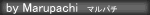- 2021年5月
- 2020年8月
- 2020年6月
- 2020年5月
- 2019年1月
- 2018年8月
- 2018年6月
- 2018年5月
- 2018年3月
- 2018年1月
- 2017年12月
- 2017年11月
- 2017年10月
- 2017年9月
- 2017年8月
- 2017年7月
- 2017年6月
- 2016年11月
- 2013年9月
- 2013年8月
- 2013年6月
- 2013年5月
- 2013年4月
- 2013年3月
- 2013年2月
- 2013年1月
- 2012年12月
- 2012年11月
- 2012年10月
- 2012年9月
- 2012年6月
- 2012年5月
- 2012年4月
- 2012年2月
- 2011年7月
- 2011年5月
- 2011年4月
- 2011年2月
- 2010年12月
- 2010年11月
- 2010年10月
- 2010年9月
- 2010年8月
- 2010年7月
- 2010年6月
- 2010年5月
- 2010年4月
- 2010年3月
- 2010年2月
- 2010年1月
- 2009年12月
- 2008年2月
- 2008年1月
- 2007年12月
- 2007年5月
- 2007年4月
- 2007年3月
- 2007年2月
Epic Online Services のSDKをSwiftから使う / magicien
Epic Online Services のサンプルをMacでコンパイルして動かすの続き。Epic Online Services のMac向けSDKは、dylib(動的ライブラリ)の形で配布されており、Swiftから直接使うことができない。Swiftから、このライブラリを使うための手順は次の通り。
普通のdylibなら、module.mapとXcodeのパス設定追加でSwiftから使えるようになる。
1. ライブラリ用ファイル構成
Xcodeで作ったプロジェクトの中にライブラリ用ディレクトリを作る。プロジェクトルート/ ┗ Frameworks/ ┗ EOSSDK-Mac-Shipping/ ┣ libEOSSDK-Mac-Shipping.dylib (ダウンロードしたSDKの SDK/Bin/libEOSSDK-Mac-Shipping.dylib をコピー) ┣ module.map (後で作る) ┗ Headers/ (ダウンロードしたSDKの SDK/Include をディレクトリごとコピー) ┣ eos_achievements.h ┣ ...
2. libEOSSDK-umbrella.h を作る
インポートするヘッダをまとめたファイルを一つ作る。基本的に全てのヘッダファイルを記載するのだけれど、後述 (6.) のエラー対応のために "eos_ui_keys.h" と "eos_result.h" を除外する。
3. module.mapを作る
これは基本的にテンプレート通り。"EOSSDK" がSwiftからimportするときの名前になる。4. libEOSSDK-Mac-Shipping.dylib をプロジェクトに登録する
libEOSSDK-Mac-Shipping.dylib をXcodeにドラッグ&ドロップする。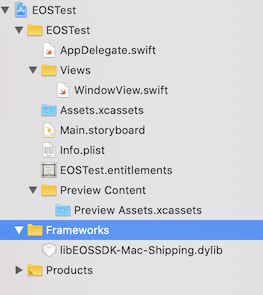
TARGET の Frameworks, Libraries, and Embedded Content に libEOSSDK-Mac-Shipping.dylib が登録されていることを確認(無ければドラッグで追加)し、Embed & Sign (または Embed Without Signing)に設定する。
5. パス設定追加
プロジェクトのパス設定を追加する。・Search Paths > Library Search Paths
"$(PROJECT_DIR)/Frameworks/EOSSDK-Mac-Shipping" を追加
・Swift Compiler - Search Paths > Import Paths
"$(PROJECT_DIR)/Frameworks/EOSSDK-Mac-Shipping" を追加
6. EOSのヘッダファイルを修正
本来ならこの段階で使えるようになるが、clangのプリプロセッサの問題なのか、一部ヘッダでエラーが出るので修正する。規約に引っかかりそうなので、修正後のファイルを載せないが、次のように修正する。
・eos_ui_types.h
eos_ui_keys.h の中身を丸ごとコピーして 101行目の 「#include "eos_ui_keys.h"」 の部分にペースト
・eos_common.h
eos_result.h の中身を丸ごとコピーして 15行目の 「#include "eos_result.h"」の部分にペースト
・eos_ui_keys.h を削除
・eos_result.h を削除
7. 使う
module.map に設定した名前でインポートする。import EOSSDK
今回はここまで。
続き:Epic Online Services のSDKでログインするまでの流れ(Swift)
この記事のURL: https://darkhorse2.0spec.jp/266/
2020/05/24(Sun) 20:35:54
JoyKeyMapper: SwitchのJoy-ConとProコントローラをMacで使うツールを作った / magicien
タイトルの通り、SwitchのJoy-ConとProコントローラをMacで使うツールを作りました。JoyKeyMapper(App Store)
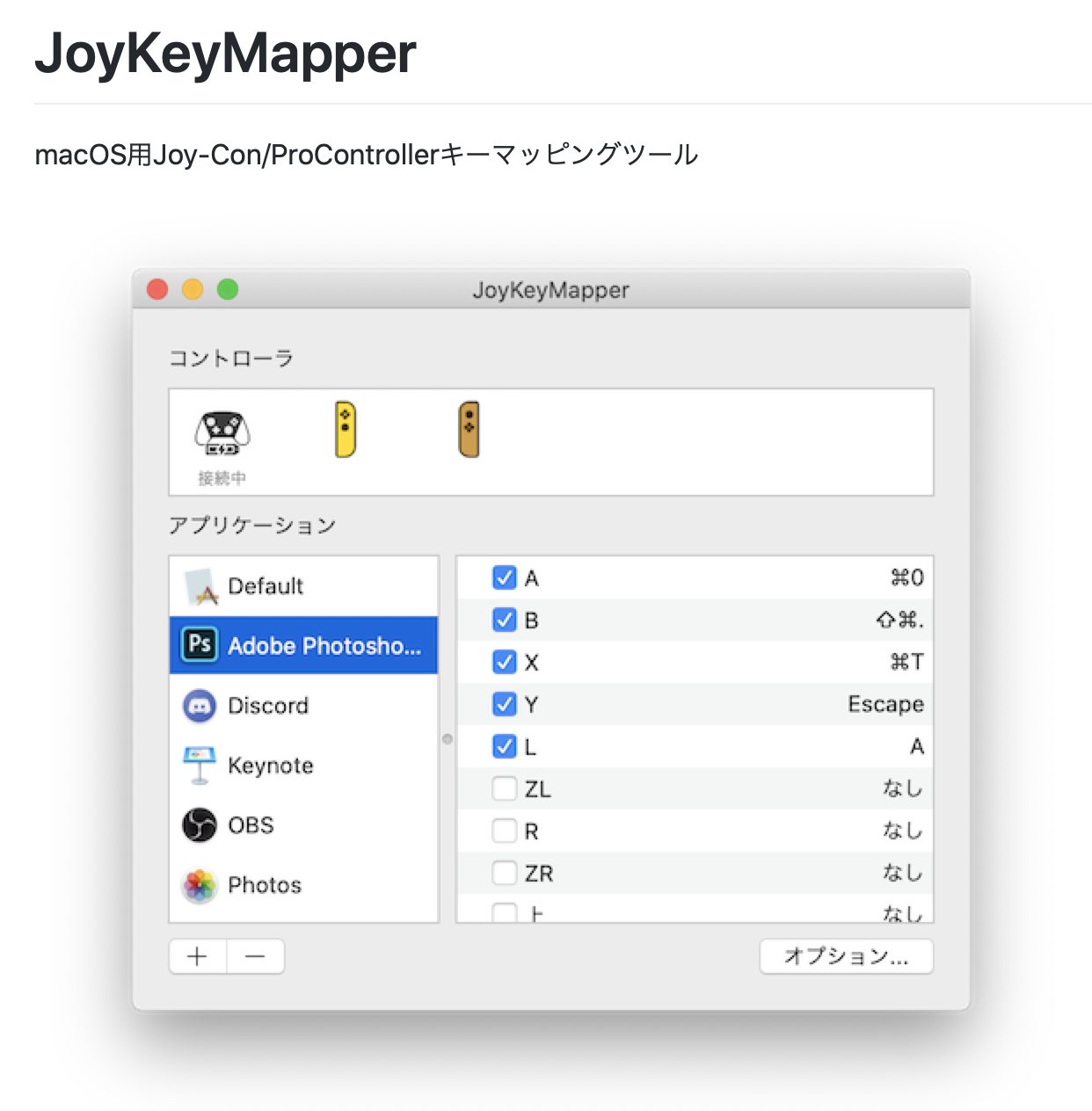
オープンソースなので、Githubでソースコードを公開しています。
詳しい使い方もGithubの方に書いたので、そちらをご覧ください。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/265/
2020/05/21(Thu) 20:20:39
Epic Online Services のサンプルをMacでコンパイルして動かす / magicien
ご無沙汰しております。まさか5月にもなって2020年初、どころか令和初投稿です。先日、Epic Games から Unreal Engine 5 の映像が公開されて話題になりましたが、個人的には、ユーザアカウント管理が無料でできる Epic Online Services の方が気になったので、Macでサンプルを動かしてみました。
以下、Macでサンプルを動かすまでの手順を書いておきます。
大まかな手順は Quick Start Guide を参照。
1. Developer Portal のユーザ登録
ユーザ登録がまだの人はまず登録から。Epic Games のユーザと共通。ログインページ
2. SDK&サンプルのダウンロード
Developer Portal からSDKをダウンロードする。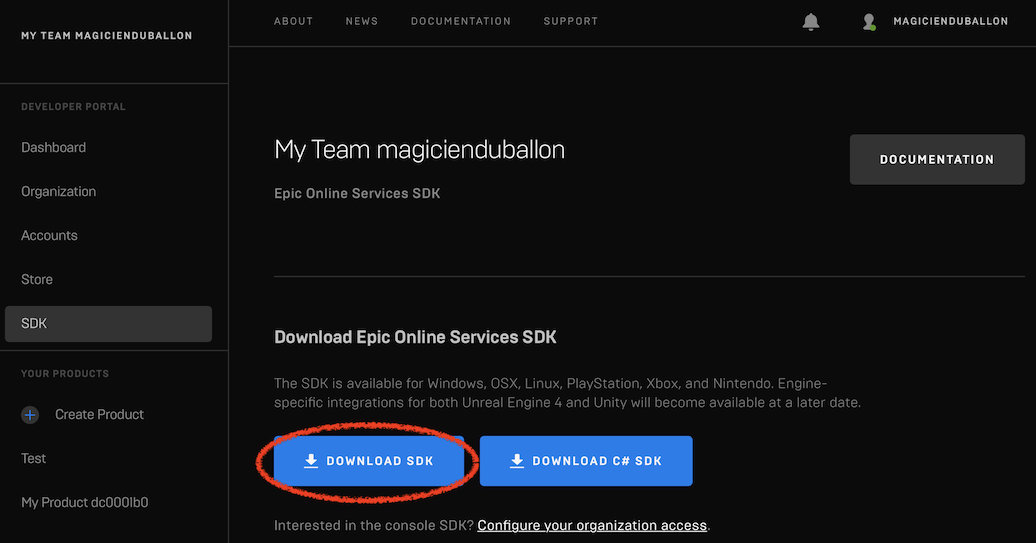
ダウンロードしたSDKの中にサンプルコードも入っている。
3. 必要なライブラリ等のインストール
・Xcode(とコマンドラインツール):App Storeからインストール・Homebrew:Homebrewのサイトにあるコマンドをコピペして実行
・SDL2:Homebrewでインストール。
brew install sdl2
・SDL2_ttf:Homebrewでインストール。
brew install sdl2_ttf
・GLEW:Homebrewでインストール。
brew install glew
・cmake:Homebrewでインストール。
brew install cmake
4. サンプルの一部修正(いらないかも)
自分の環境だと cmake で GLEW の読み込みがうまくいかない(GLEW_LIBRARIES 等の変数が設定されない。cmakeの仕様、というかバグだと思う)ので、サンプル内のCMakeLists.txt の内容を一部修正する。(cmake自体を直してしまってもいいかもしれない)find_package(GLEW)を次のようなコードに置き換える。(例えば、Samples/SimpleFramework/CMakeLists.txt の場合は76行目)
find_path(GLEW_INCLUDE_DIR GL/glew.h
/usr/local/include
/System/Library/Frameworks/GLEW.framework/Versions/A/Headers
${OPENGL_LIBRARY_DIR}
)
find_library(GLEW_LIBRARIES GLEW
/usr/local/lib
/usr/openwin/lib
/usr/X11R6/lib
/usr/local/Cellar/glew/2.1.0_1/lib
)
if (DEFINED GLEW_LIBRARIES)
message(STATUS "GLEW found")
set(GLEW_FOUND TRUE)
endif()
修正後のCMakeLists.txtの例。glewのパス "/usr/local/Cellar/glew/2.1.0_1/lib" のバージョンは各自の環境に合わせて変更してください。バージョン番号を埋め込んでいるのであくまで応急処理。5. サンプルのビルド
chmod 755 ./Build.shでビルド用シェルに実行権限を付与。
./Build.shでビルド。エラーが出ずにビルドが完了すればOK。
6. アプリの設定
ここで一旦 Developer Portal に戻ってアプリの設定をする。詳しい手順は Getting Started with Epic Account Servicesを参照。
6.1. Productの作成
アカウント作成時に「My Product xxxxx」というProductがデフォルトで出来ているようなので、それを使っても良い。新しく作る場合は、「Create Product」から。後で気づいたけど、現状、作成したProductを消す術が無いようなので無闇に作らない方が良いかもしれない。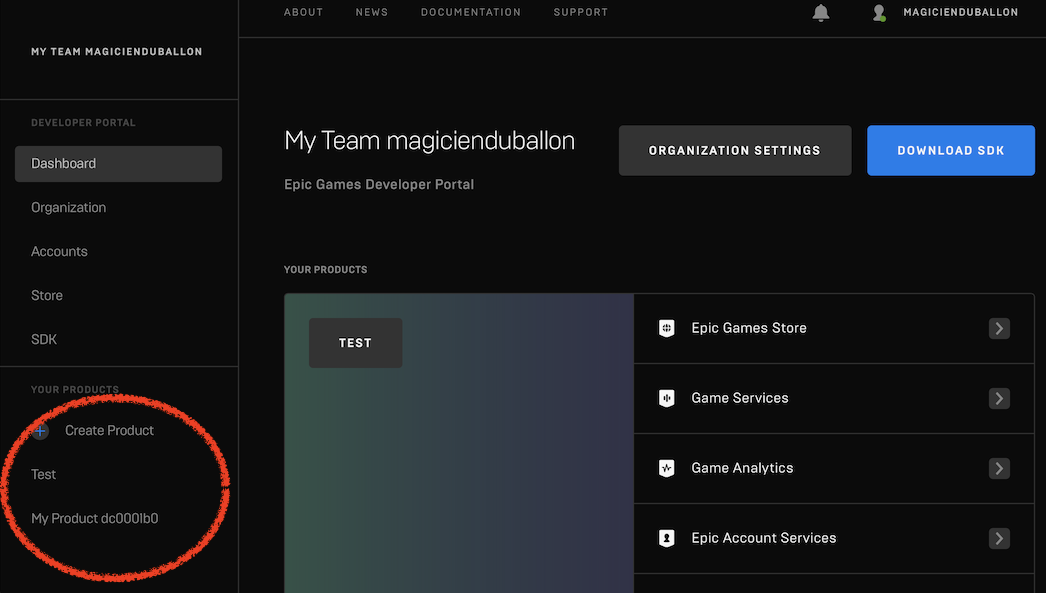
6.2. Clientの作成
Product Settings > Client Credentials > NEW CLIENT でクライアントを作成。FEATURESはとりあえず全部付けておく。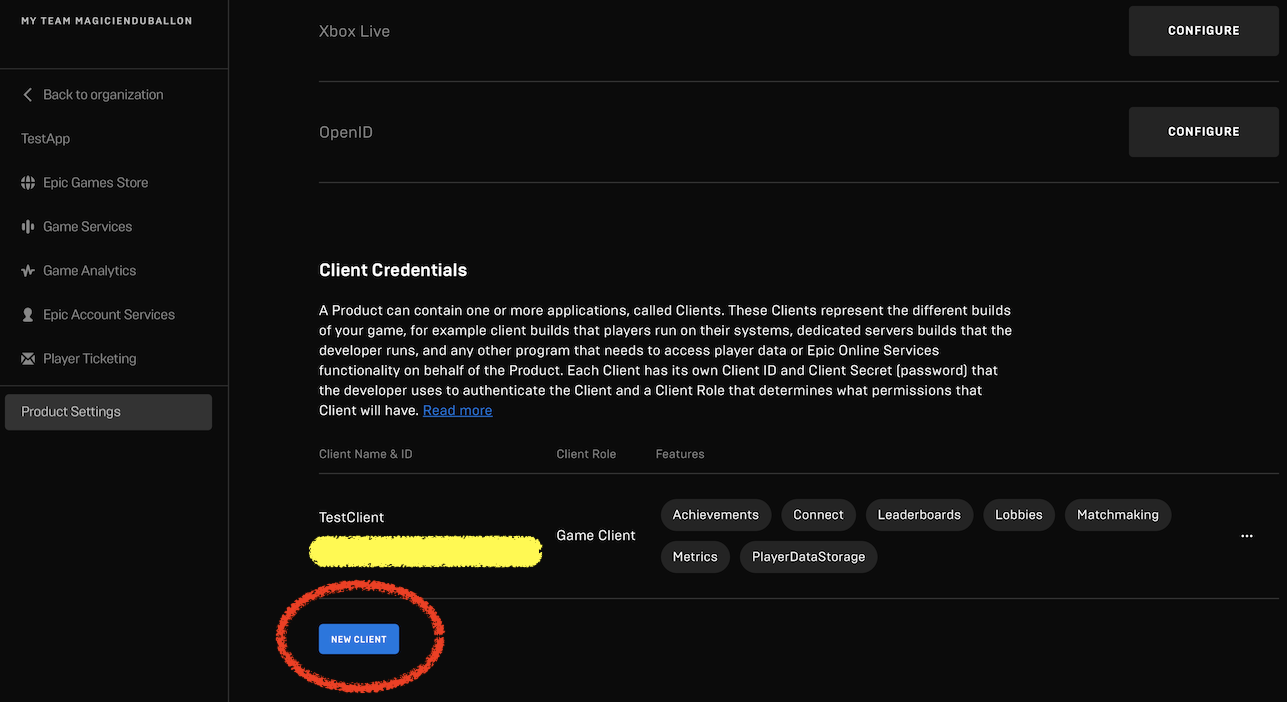
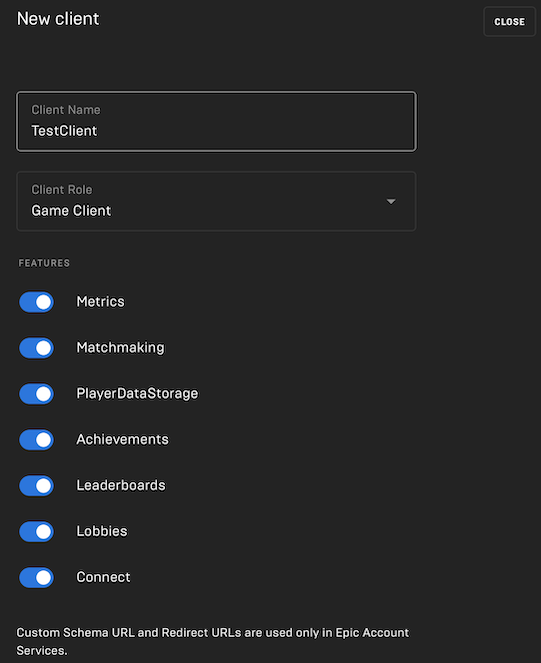
6.3. Epic Account Servicesの設定
作ったProductのEpic Account Servicesの設定をする。・Brand Settings:Privacy Policy URL が必須。テスト用で公開するつもりがないなら、適当に自分の持っているURLか何かで埋めれば良いと思う。自分は App Privacy Policy Generatorで自動生成したものをGistに貼り付けた。実物はここ。
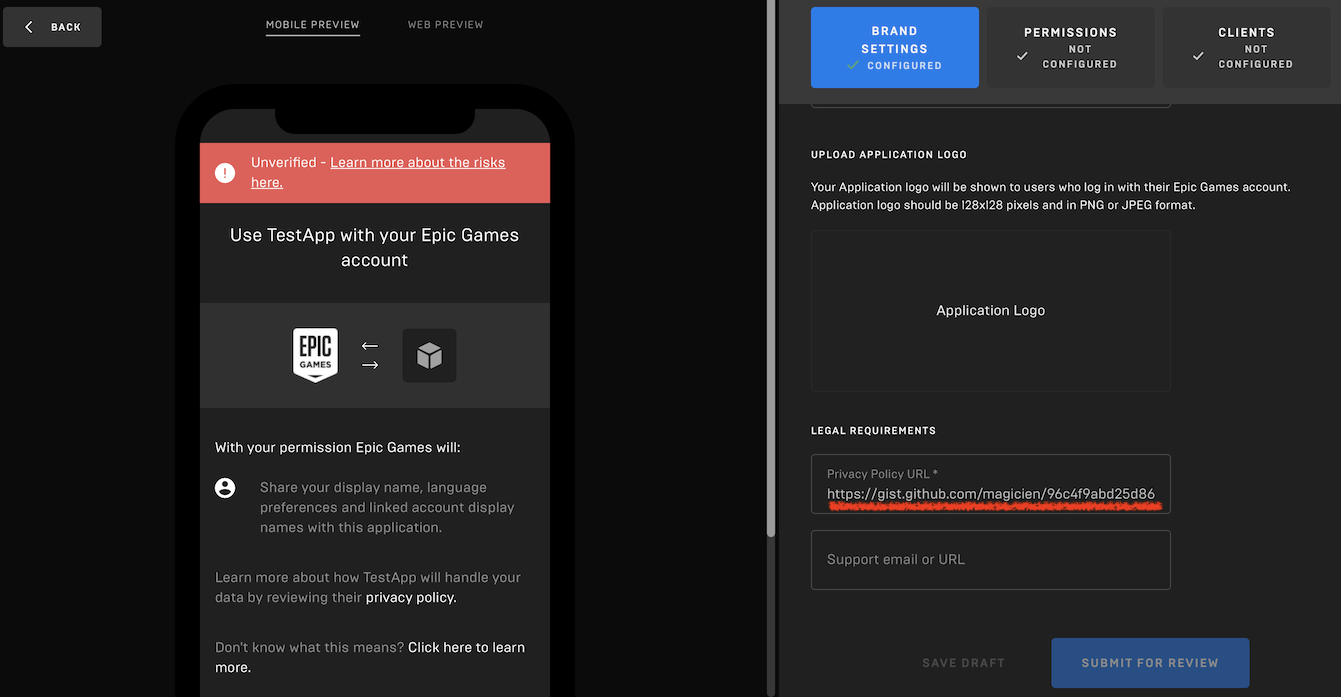
「SUBMIT FOR REVIEW」ボタンがあるけど、アプリの審査はまだないっぽい。
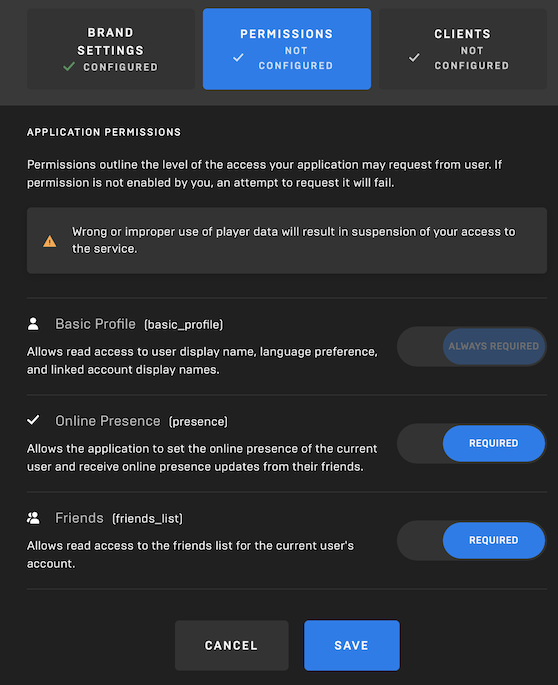
・PERMISSIONS:全部試したいので全部REQUIREDにする
・CLIENTS:6.2. で作成したClientを選ぶ
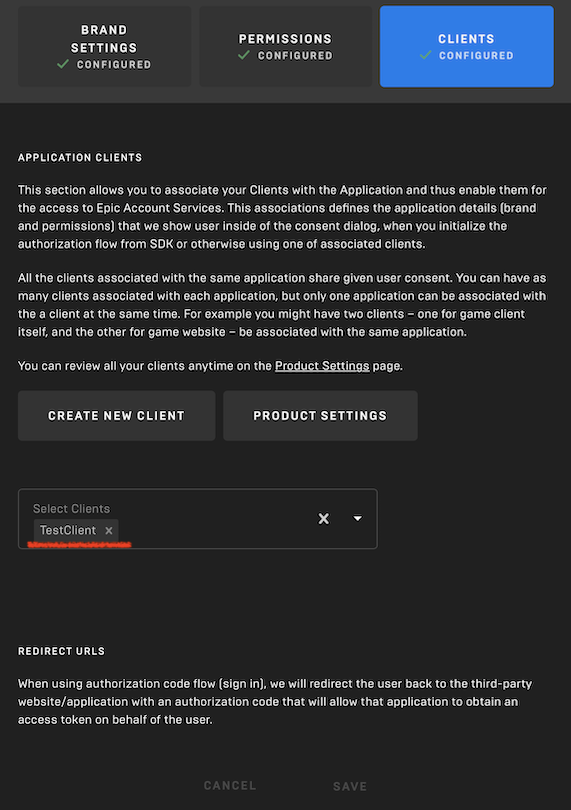
3つとも CONFIGURED になればOK。
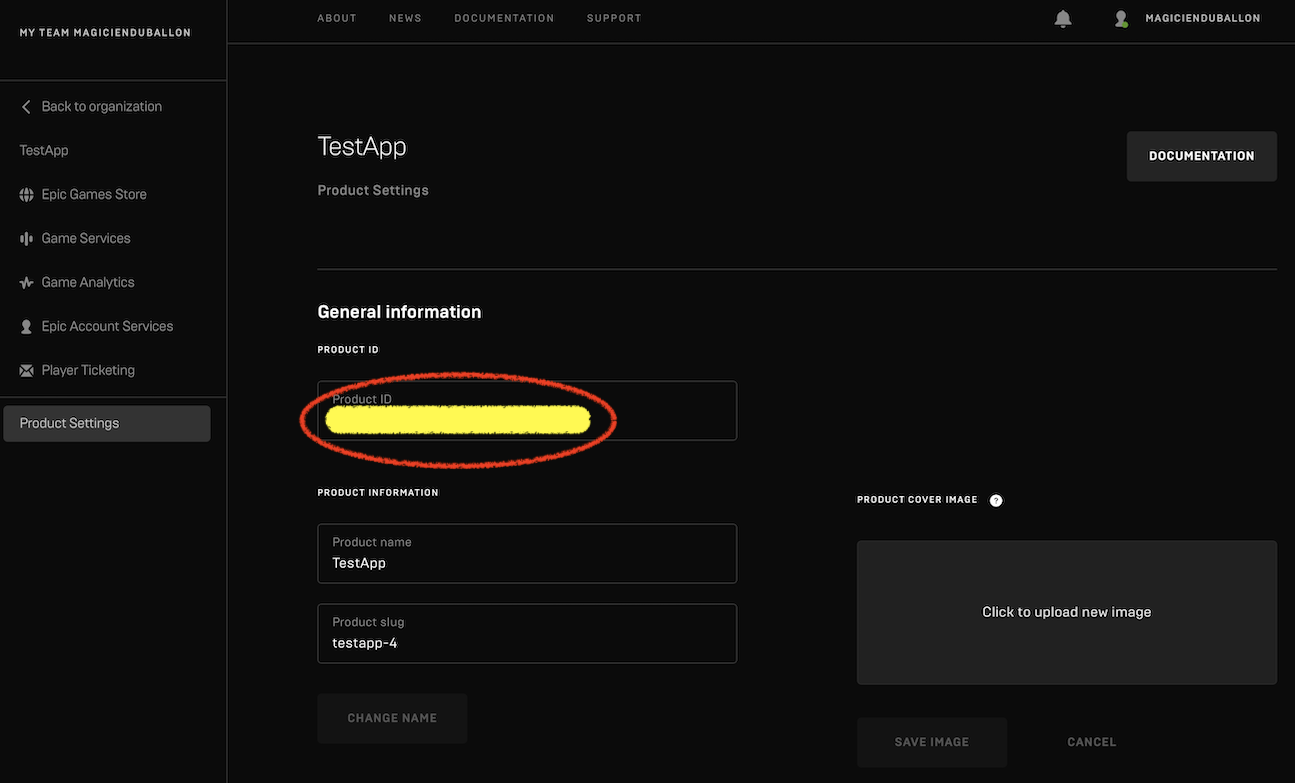
6.4. Product情報を集める
"Product Settings" のページからサンプルの実行に必要な情報を集める。・Product ID
・Sandbox ID
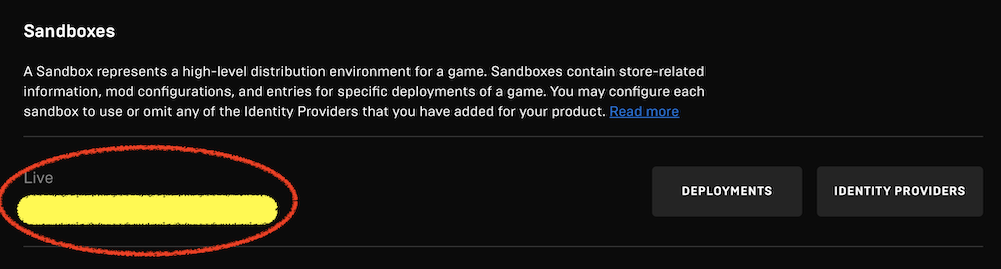
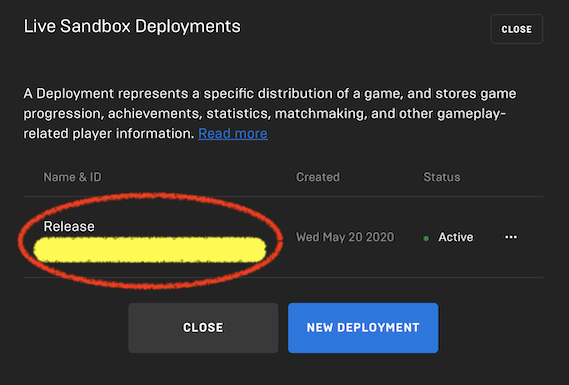
・Deployment ID:Sandboxesの DEPLOYMENTS から
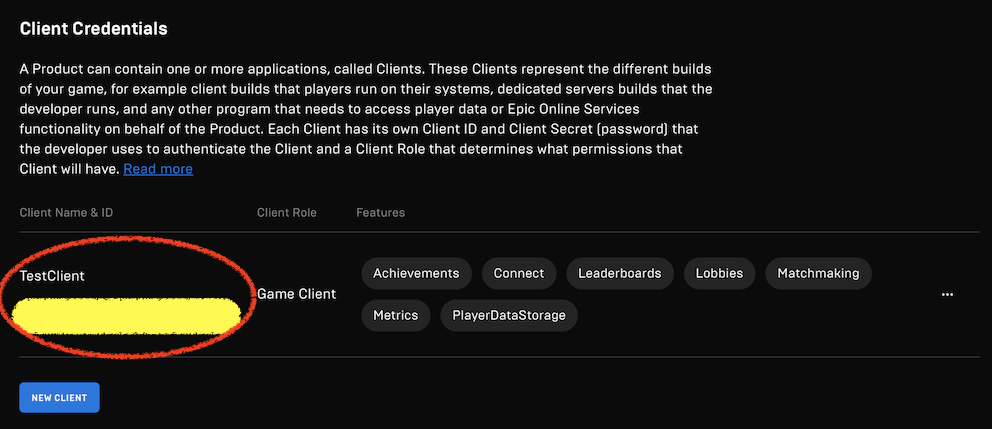
・Client ID
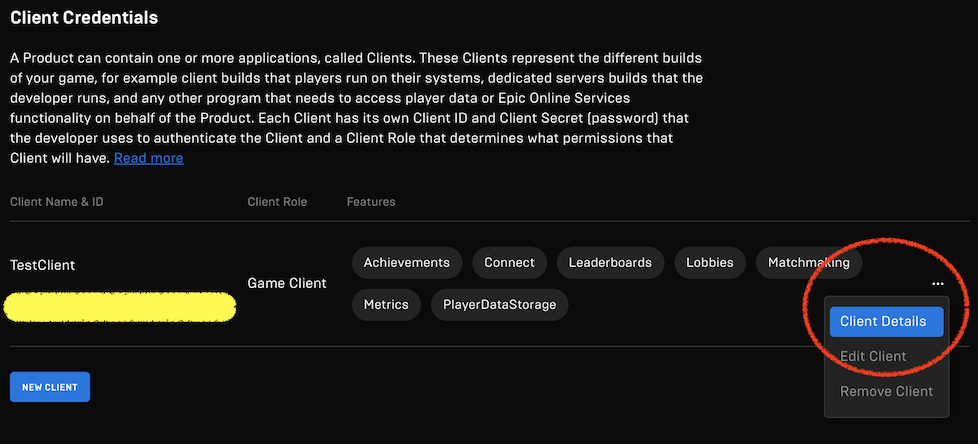
・Client Secret:三点リーダーのメニュー内のClient Detailsから。"Copy secret key" でキーをコピーする。
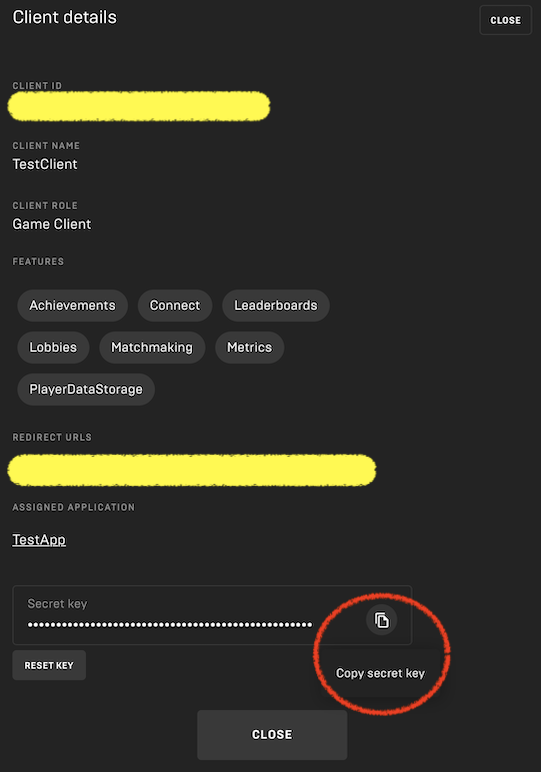
7. サンプル実行用シェルの修正
・Run.sh を編集して実行時の引数を追加する。6.4. で集めたIDを引数として渡す。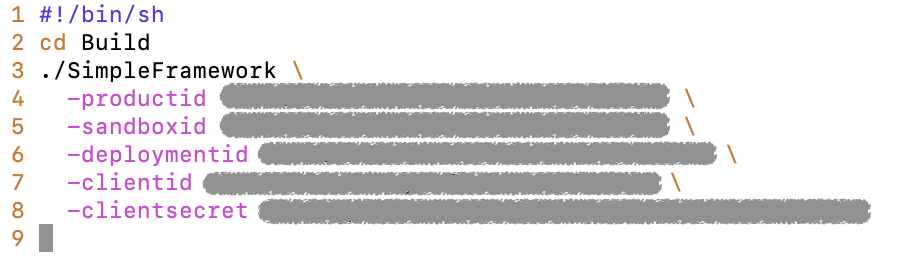
chmod 755 Run.shで実行権限を付与。
8. サンプル実行
./Run.shで実行。
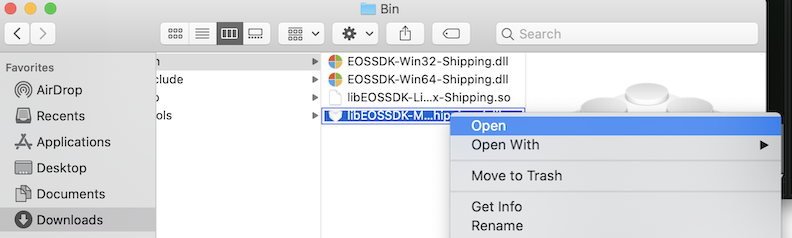
・ファイルの信頼性のエラーが出た場合
うろ覚えだけど、実行時に SDK/Bin/libEOSSDK-Mac-Shipping.dylib の信頼性でエラーが出た気がする(App Store以外からダウンロードしたファイルを実行しようとしたときに出るあれ)。その場合は、ライブラリを右クリック(Ctrl + クリック)して Open を選択して一度ファイルを開けばエラーが出なくなる。
・アプリ起動後、Account Portal > LOG IN を選ぶとブラウザが開いてログインページに飛ぶ。
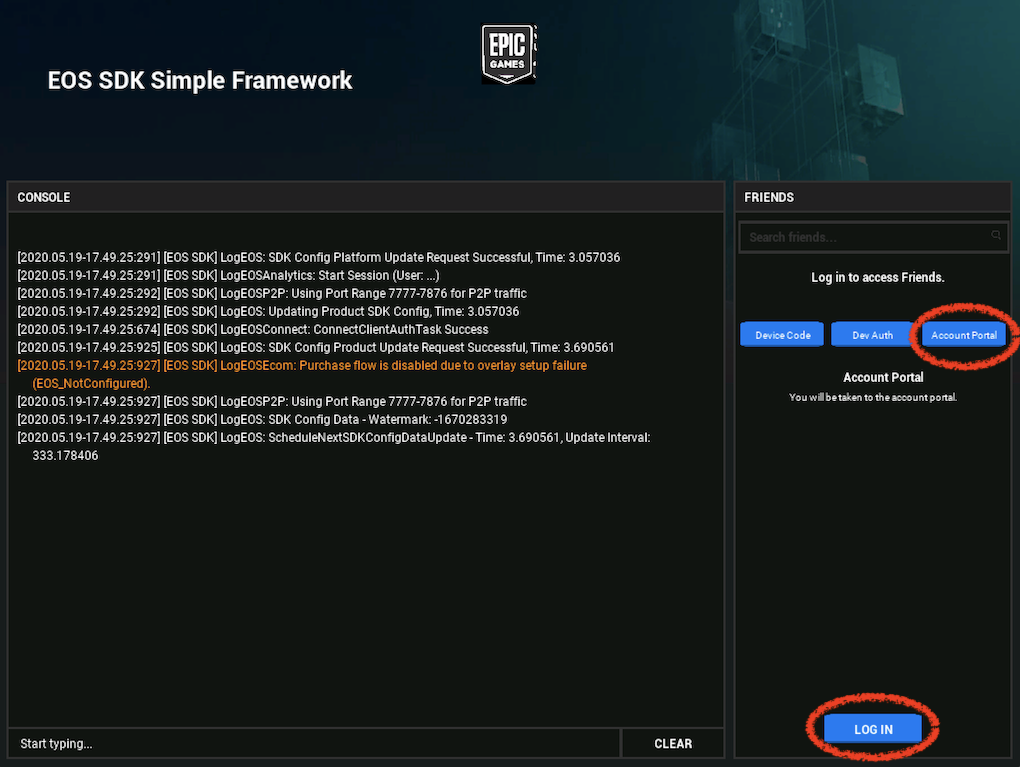
・審査前なので、Unverified Application の警告が出るが、気にせず CONTINUE TO APP を選ぶ
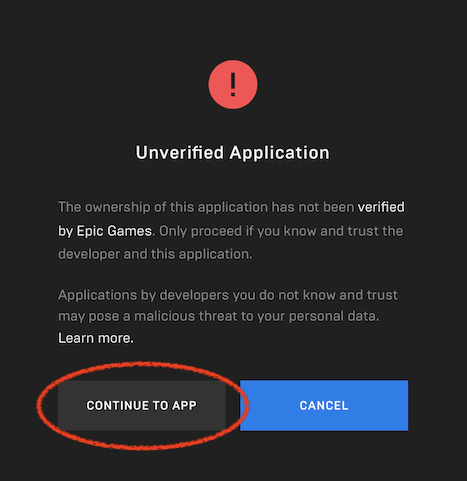
・ALLOW を選ぶ

・サンプルのログインが完了し、ユーザ名が表示される。
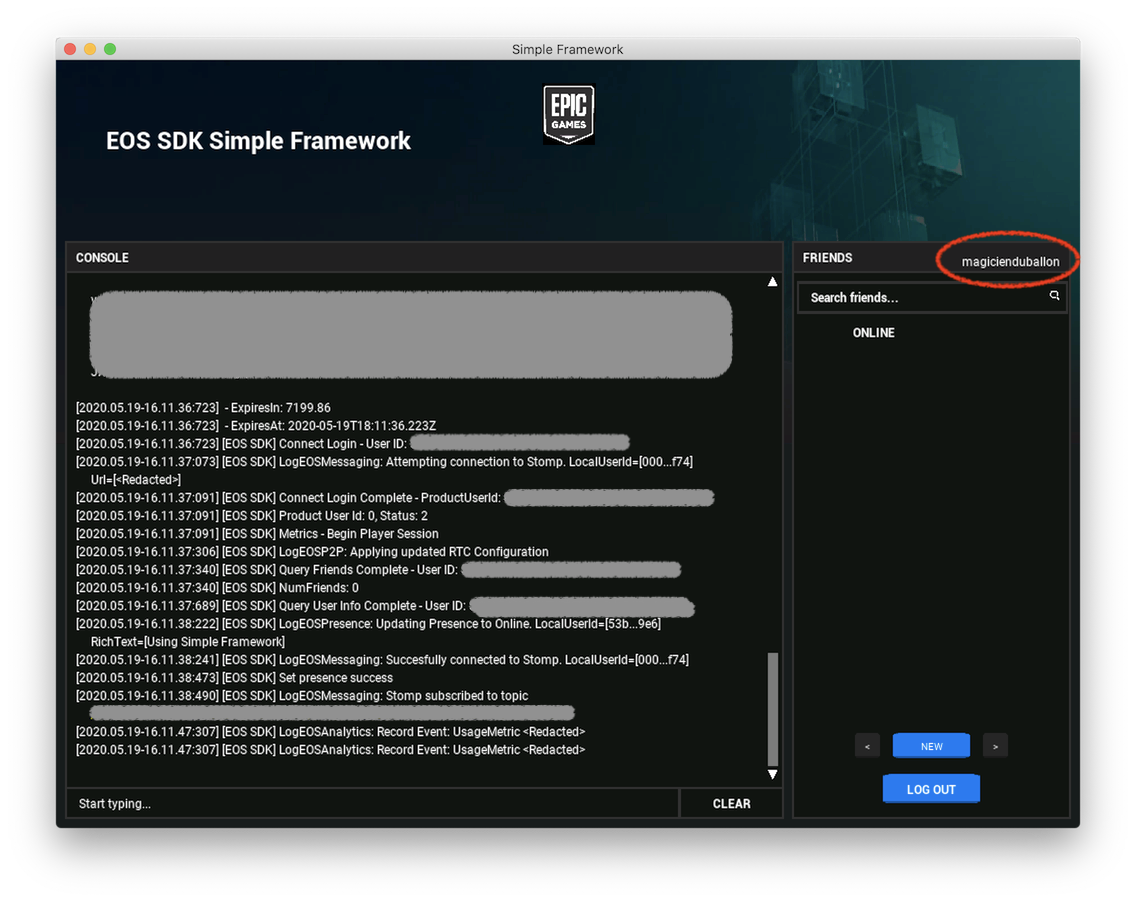
今回はここまで。
続き:Epic Online Services のSDKをSwiftから使う
この記事のURL: https://darkhorse2.0spec.jp/264/
2020/05/20(Wed) 03:02:10
あけましておめでとうございます / magicien
生きています。昨年の目標を見返してみたら、ほぼ達成できていませんでした。
vtuberが楽しすぎて、年始早々に軌道がずれていったようです。
2019年は昨年のような熱に浮かされた感じから徐々に落ち着いていくと思うので、目標達成率も上がるでしょう。
そんなわけで2019年の目標。
- サイト引越し
- vtuberデビューする
- glTF/VRM で何かしら貢献する
- SceneKit/ARKit で何かしら貢献する
- アプリ開発頑張る
- VR機器買って何か開発する(QuestかCosmosか...)
- 動画関連のソフトかサービスを作る
- 誰かと共同で何か作る
- 風邪をひかない(花粉症は仕方ない)
- 週次で何かやる
目標にする分野の範囲が狭すぎる。また今年も新しいものが出てくると思うので、その時に目標を考えよう。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/263/
2019/01/12(Sat) 16:36:02
VRMのページにVRMQuickLookが追加されていた / magicien
気づいたら、VRMのページにVRMQuickLookが追加されていました。ありがとうございます!で、さらに気づいたら、VRMQuickLookをこのサイトで公開するのを忘れていました。
GitHubに公開しただけで満足してしまった...
VRMQuickLook:macOS、VRM用QuickLookプラグイン
実際のところ、VRMPreviewに、このVRMQuickLookが組み込まれているので、VRMPreviewをインストールしている場合は、こちらを別途インストールする必要は無いです。
以上、雑な紹介でした!
この記事のURL: https://darkhorse2.0spec.jp/262/
2018/08/18(Sat) 15:59:13
Mac用VRMビューアを公開しました / magicien
 ご無沙汰です。ここ数週間ほどでVRMがにわかに盛り上がってきているので、iOSのアプリ開発を一旦放り出してVRMビューアを開発していました...
ご無沙汰です。ここ数週間ほどでVRMがにわかに盛り上がってきているので、iOSのアプリ開発を一旦放り出してVRMビューアを開発していました...ダウンロードはGitHubから。
実のところ、以前作ったglTF向けのライブラリをほぼそのまま使っているだけで、VRM専用のデータはほとんど使っていません。
やっているのは、シェーダの差し替えと、VRMのメタ情報の読み込みくらい。
VRMのシェーダのうち、VRM/MToon だけはマルチパスシェーダのため未対応。SceneKitの場合、マルチパスシェーダはビューかカメラかライトにしか設定できないはず(APIが変わっていなければ)なので、マテリアル毎の設定は難しいのです。
シェーダ内で毎回分岐させるのは抵抗があるので、やるとすれば MToon用のカメラを別途用意する感じでしょうか。デプスバッファや影の処理がうまくできるのかは怪しい。
紹介動画は時間があるときに作る...
タグ:
この記事のURL: https://darkhorse2.0spec.jp/261/
2018/08/14(Tue) 03:17:32
WWDC2018のKeynoteメモ / magicien
Keynoteに一時間遅刻してしまった...ギル様を優先したとも言う。別言語で2窓は流石に無理だった。まだまだ修行が必要。ただ、2時間のライブであれば、1時間の遅刻は遅刻にはならない。
YouTubeには便利な機能があって、ライブ中でも1時間遅れで再生出来るので、倍速で再生すれば、1時間後には最新の映像に追いつけるという寸法である。
さて、3D好きとしては、やはりARKit2に注目したい。
複数の端末で一つのAR空間を共有出来るのは非常に嬉しい。
背景を実写ではなく3Dモデルにすれば、VRも出来るので、顔認識用の人数分のiPhoneXとカメラモーション用のiPhone端末が用意できれば、同じVR空間で複数のVTuberがわちゃわちゃ動き回る様をライブ配信出来るようになりそう。ネット越しの同期もサポートしてくれるなら、物理的に集合する必要はない。出演者だけではなく、観客も同じ空間に入り込んで自由に動き回れる。どこまで出来そうかは後でAPIを確認しよう。
→確認した結果、ネット越しだとあんまり使えなさそう。表情の変化をリアルタイムに反映するのもだいぶ頑張らないといけないようだ。ライブラリにお任せ出来ると思ったのに、結局自分で実装しないといけないのか。
usdzというファイル形式は、usdの拡張でzip対応しているっぽい。ネット経由での利用を意識してのものだと思うので、glTFと競合していくことになるのかな。個人的にはVRMがglTFの公認拡張仕様になってglTFが流行って欲しい。
正直、他に気になるものがあまり無かった。あとはSessionのスケジュールを見て気になるものを選んで見ていけば良いかな、と考え中。ReplayKit 2、HLS、ARKit 2、Ray Tracing、Video Effects Using Depthあたり。MapKit JSも地味に気になる。あとはかなり望み薄だけど、SafariがWebGL2、GLES3に対応する気があるかどうか。
→OpenGL ESがdeprecatedって書いてある!WebGLをどうするつもりなんだ。
そういえば、MicrosoftがGitHubを買収するとかなんとか。アメリカのIT企業は他社のイベントに爆弾を放り込むノルマでもあるんですかね...
タグ:
この記事のURL: https://darkhorse2.0spec.jp/260/
2018/06/05(Tue) 05:00:54
バーチャルYouTuberになれるアプリ「Showar」をリリースしました / magicien
前々から作っていたARKitを使ったアプリが、ようやく公開出来ました。アプリの名前は、Showar(シャワー)です。
ダウンロードはこちらから↓
https://itunes.apple.com/jp/app/showar-3d-vr-ar-avatar/id1369578518
バーチャルYouTuberとか言っておきながら、ニコ動だけに投稿するのもおかしな話だと思ったので、YouTubeにも動画アップしておきました。
ところで、今更ですが、ぽんぽこ24時間生放送お疲れ様でした。出演者の方々はもちろん、視聴者の皆さんも。
最近、ただでさえ睡眠時間が削られているところに24時間生放送をぶっこんでくる鬼畜さに惚れました。
この記事のURL: https://darkhorse2.0spec.jp/259/
2018/05/05(Sat) 22:34:43
MMDSceneKitをCocoaPodsに対応させた / magicien
1ヶ月ぶりです。2月はにわかに忙しくなってアプリ開発が全然進まず。3月はペースを戻していきたい所存。それはさておき、MMDSceneKitをCocoaPodsに対応させました。
なぜCocoaPodsに対応させたかというと、今作っているiOSアプリにMMDSceneKitを組み込んだところ、ダイナミックライブラリを入れないで!とAppleから怒られたから。
それならソースからコンパイルすれば良いのだろう、ということでMMDSceneKitのプロジェクトを丸ごとワークスペースに取り込んでみたものの、細々とエラーが出て面倒くさい。 なぜだ!CocoaPodsで入れた他のライブラリは問題ないのに・・・と考えた結論は、MMDSceneKitだけCocoaPodsを使っていないから(思考停止)。
頑張れば手動でもうまく組み込めるんだろうけど、頑張らないと使えないフレームワークとはいったい・・・うごごご!
そんな感じです。そのうちCarthageにも対応するかもしれない。
この記事のURL: https://darkhorse2.0spec.jp/258/
2018/03/04(Sun) 21:21:13
macOSをアップデートしたら辞書データが消えました / magicien
Missing dictionaries for Dictionary app in 10.13.4 beta (17E139j)バージョンは、10.13.4 Beta 1。辞書をよく使う人は次のバージョンが出るまでアップデートを待った方が良いかもしれない。
割と使っているから早く直してくれ〜。AppleのQAチームが息してないぞ。
追記:手動でデータをダウンロードして復旧できた。原因は辞書データのダウンロード先がhttpであること(httpsではないこと)な気がする。
/System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xml に辞書一覧が入っているようだったので、
$ plutil -p /System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xmlで中身を見て、手動でデータダウンロードしたら復旧できました...
辞書一覧データの中身は配列になっていて、__BaseURL と __RelativePath をつなげたURLに辞書データが置いてある模様。
例えば、ウィズダム英和辞典の場合は、
11 => {
"__BaseURL" => "http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/"
"__CanUseLocalCacheServer" => 1
"__InstallWithOS" => 1
"__RelativePath" => "com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zip"
"_CompatibilityVersion" => 5
"_CompressionAlgorithm" => "zip"
"_ContentVersion" => 5
"_DownloadSize" => 29800639
"_IsZipStreamable" => 1
"_MasteredVersion" => "2610"
"_Measurement" => <41bb8766 3a4e0a5f a296262d 5fd506a4 bae32e1e>
"_MeasurementAlgorithm" => "SHA-1"
"_UnarchivedSize" => 33202176
"Countries" => [
0 => "JP"
]
"DictionaryCopyright" => "ウィズダム英和辞典 / The Wisdom English-Japanese Dictionary <br/> Copyright © 2007, 2013 Sanseido Company Ltd., under licence
to Oxford University Press. All rights reserved. <br/><br/> ウィズダム和英辞典 / The Wisdom Japanese-English Dictionary <br/> Copyright © 2007, 2013 Sanseido
Company Ltd., under licence to Oxford University Press. All rights reserved."
"DictionaryIdentifier" => "com.apple.dictionary.ja-en.WISDOM"
"DictionaryPackageDisplayName" => "ウィズダム英和辞典 / ウィズダム和英辞典"
"DictionaryPackageName" => "Sanseido The WISDOM English-Japanese Japanese-English Dictionary.dictionary"
"DictionaryType" => "Bilingual"
"FormatVersion" => 2
"IndexLanguages" => [
0 => "ja"
1 => "en"
]
"Language" => "ja"
}
となっているので、辞書データは
http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zipにある、という感じです。
ダウンロードしたzipファイルの中にある、〜.dictionary というファイルを ~/Library/Dictionaries/ に放り込んで、辞書アプリの環境設定から使う辞書に指定してあげればOK。
抽出したURL一覧を置いておきます。
辞書一覧
macOS用
Apple DictionaryPolitikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer's Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Dicionário de Português licenciado para Oxford University Press
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük
iOS用
Apple DictionaryPolitikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer’s Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Oxford Portuguese Dictionary - Português-Inglês • Inglês-Português
Dicionário de Português licenciado para Oxford University Press
Oxford Russian Dictionary - Русско-Английский • Англо-Русский
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük
タグ:
この記事のURL: https://darkhorse2.0spec.jp/257/
2018/01/28(Sun) 15:05:08