しぐれういさんの個展に行った / magicien　

気づいたら3年半以上更新するのを忘れていた。仕事ばかりしていると、書けることが無くなってしまっていけない。先日、しぐれういさんの個展に行ったので、その日のことを書き残しておこうと思う。これは備忘とリハビリとサイトの動作確認のために、だらだらと書き連ねた自分のための文章なので、読む価値はあまり無い。

しぐれういさんは、言わずと知れたイラストレーター、そしてvtuberでもある。なぜか歌も歌っており、ある動画はYouTube上で1億再生を超えている。こうなると、もはや何者なのか分からなくなってくるが、本業はやはりイラストレーターであるということで、個展を開くという。

個展は六本木で開かれていた。週末、近くへ外出の予定があったため、ついでに寄ってみようと思い、昼に六本木の駅を降りた。9月の半ばになっても夏が我が物顔で居座っており、ヒルズに着く頃には汗が吹き出していた。遠目に長い行列が見えて嫌な予感がしていたのだが、近づいてみると案の定、個展の入場列ができている。このまま列に並ぶと、汗で全身びしょびしょの妖怪が個展会場に現れてしまう。入場までどれくらいかかるかもわからない。仕方ないので、個展は断念して本来の用事を先に済ませることにした。

平日に再挑戦しようとも考えたのだが、六本木はもしかして平日の方が人が多いかも知れないというのと、前職の関係者にばったり出くわしたらなんか嫌だなという思いがよぎり、夕方に再度個展会場に行ってみることにした。すると、入場列はなくなり代わりに整理券を配るスタッフが立っていた。薄暗くなった会場周辺では、個展の入り口を背景に写真撮影をしている人たちが多くいて、昼間とはまた違った雰囲気になっている。整理券を受け取り、数十分ほど森美術館の売店を冷やかした後、もう一度会場に行くと、すんなりと入場できた。

会場はシンメトリー、というか円形になっていて、半分がイラストレーター、もう半分がvtuberをテーマにした絵が並んでいる。個展というものにあまり行ったことがなかったため、それぞれの絵に値札が付いているのを見て、そういえば絵って買えるのかと、ふと思う。入り口に飾られている立体造形は 5,550,000 円となっていて、ほぼ原価だという。自分が個展を開いたらきっと破産してしまうだろう。

物販の列が出来ていることを除けば、会場内は思ったより混雑していなかったが、そこまで広々としたスペースがあるわけでもなく、自然、絵を至近距離から眺めることになる。考えてみると、パソコンで絵を観るときはもっと近いんだったと思いつつ、ディスプレイよりも大きなサイズのデジタル絵をどうやって描いたのだろうと思案する。会場内は暗めで、見上げると青や黄色のライトが絵に光を投げかけている。仕掛けのある絵が多く、光がオーロラのように反射したり、上層の絵が下層に影を作ったりと、リアルだからこその展示ばかりで、そういえば、しぐれういさんは美大出身であることを思い出した（高校生のはずだけど）。

この個展は、vtuberデビュー5周年企画の一部でもあり、同じく5周年企画で発売されたCDのジャケット絵も飾られていた。このCD自体にも数多くの著名なアーティストが関わっていて、CDを買ったときは、随分とどでかいことをしたな、とびっくりしたものだ。しかし、個展に並ぶ絵の一つとしてCDジャケット絵があるのを見ると、どでかく感じたCDは世界の一部で、外側にさらに大きな世界が広がっていることを思い知らされて呆然とした。

vtuberサイドには、様々なvtuberの絵が並んでいた。中でも目を惹いたのは、にじさんじのリゼ・ヘルエスタさんを描いたもの。背景が一部透明になっている絵に複数のライトが当たっていて、後ろの壁に映る髪の影に濃淡が生まれており、それがとても有機的で魅力的だった。個展のタイトルが「雨を手繰る」なのだが、リゼさんが雨女として知られており、その偶然の関係性にも感じるところがあった。

二重円のような構造の会場の中心部には、取り囲むようにディスプレイが並んでいて、Live2Dや3Dのしぐれういさんが時折、歩いたり座ったりする姿を見せる。上には大きな傘がかかっていて、雨が傘を叩く音が聞こえてくる。天井の青いライトは、この傘に空と雲を投影するためのものだったようだ。学校のチャイムと雨音をモチーフにしたようなピアノがBGMとして流れており、チルい。空調のおかげで温度的にもチルい。おかげで会場をぐるぐると何周もして、数々の絵と快適な空調に別れを告げられずにいた。

ゾーンはリアルのイラストレーターとバーチャルのvtuberとで分かれていたものの、何周もしているうちにその境目が曖昧に感じるようになった。影が光から生み出されるように、フィクションもリアルから生み出されたものであり、その境界は綺麗に切り分けられるものではなく、滲んで混ざる。どんなに否定しようと親子がその関係を取り消せないように、リアルとフィクションの関係は切り離せないのだ（JJ...）。CDのfictionというタイトルからそんなことを考えつつ、ゾンビのように会場を徘徊していた（疲れていたのかもしれない）。断腸の思いでようやく会場を出ると、外はすっかり暗くなっており、まだ蒸し暑い空気の向こうから微かに聞こえる虫の音は、秋の到来を予感させるものだった。

リアルで創作物に触れる機会は久しぶりで、密度の高い作品に触れると創作意欲がかきたてられる。とはいえ、絵を描くのは苦手なので、自分はコードを書いて欲を満たす他ない。最近はUnityに触れる機会が増えたので、Unityで何か作ってみたいとぼんやりと考えている。

せっかくなので、3周年記念の時に作ったファンアート的ウェブページも置いておこう。今見返してみても、我ながら頑張って作ったと思う。この時も同じように創作意欲に掻き立てられてものづくりに没頭していたのを覚えている。外からの刺激が自分へどれほど大きな影響を与えるかを今回改めて思い出すことができた。
https://magicien.github.io/CanvasInShower/

　RPGツクールMZの関数を抽出した / magicien　

ゴールデンウィークに遊ぶ用にRPGツクールMZを買った。

RPGツクールMZは、ほとんどの処理がJavaScriptで記載されていて、MacやiPhoneにも対応している優れもの。JSでプラグインを書くことで機能拡張することもできる。
プラグインは、既存の本体のスクリプト（コアスクリプト）の関数を上書きする形で拡張することになっているようだ。ただ、既存の関数の一覧がどうにも見当たらないので、関数を抽出して一覧化した。

RPGtkool MZ v1.2.1 API functions

本当は、ソースコードへのリンクも付けたかったが、ゲーム用途以外でのコアスクリプトの配布は許可されていないように思うので諦めた。パーサだけ作って配布するかもしれない。

ざっと眺めてみると、関数一つは10行以下のものがほとんどで、テストのしやすさやプラグインでの拡張性を考慮した良いデザインのように思える。本当はドキュメントをもっと充実させて欲しいけど、関数のサイズが小さいおかげで、関数名だけでどんな処理かが誤解なく伝わる場合がほとんどだろう。全体の処理の流れやクラスの依存関係がわかる資料があればそれで十分かもしれない（探せばあるかも）。

　JoyKeyMapper v1.2.0 をリリースした / magicien　

リリースしたのが1週間くらい前だったように思うのですが、こちらに書くのを完全に忘れていました。
Switch用ファミコン、スーパーファミコンコントローラに対応しました。
JoyKeyMapper

Switch用コントローラは他にNESやゲームキューブコントローラがあるのですが、こちらはまたの機会に。モンスターボールPlusはそもそもMacへの接続の仕方がよく分からなかった。もしかしたら先にリングコンに対応するかもしれない。
Joy-Conは他にも色々とセンサーが入っていて、まだまだ遊び足りないです。

　SwitchのコントローラでMIDIを再生するツールを作った / magicien　

JoyConSwiftの開発を進める中で、コントローラ振動機能をテストする必要があったので、ついでにMIDIを読み込む機能も追加してツール化しました。
ダウンロード：JoyfulPlayerのReleasesからJoyfulPlayer-vX.X.X.dmgのような名前をダウンロードしてください。

Proコンで UNDERTALE の Megalovania を再生した動画↓

技術的な解説

動画にも書いた通り、コントローラの振動は、リニア振動モーターなるものが使われており、Joy-Conには1つ、Proコンには2つ、このモーターが入っています。

学研さんと「HD振動」のヒミツについて調べてみました。 | トピックス | Nintendo

このモーターは、上下方向と左右方向でそれぞれ別の周波数で振動させることができるため、一つのモーターで同時に2つの音を発生させることができます。例えば、上下方向に 262Hz、左右方向に 440Hz で振動させると、ドとラの和音が鳴るわけです。Proコンには、モーターが2つ入っているので、最大で4和音まで再生できることになります。
実は2軸で指定できる周波数の範囲に差があり、1つは 40.88〜626.29Hz、もう1つは 81.75〜1252.57Hz が指定できるようです。音階にすると、E1〜D#5、E2〜D#6くらい。

Rumble data table

音楽の世界では、一般的に1オクターブを12分割していますが、このモーターで指定できる周波数は1オクターブにつき16段階なので、正確な音階は表現できません。今回作ったツールでは、一番近い周波数を選ぶことでそれっぽい音を鳴らすようにしています。絶対音感がある人には、とても気持ち悪いかもしれませんが、正直なところ自分には音がずれているのかどうか、よくわかりませんでした。（そもそもコントローラは楽器ではない）
課題として、特定の周波数の範囲でコントローラ全体が共鳴してしまい、うるさい、という問題があります。おそらくコントローラによって共鳴する周波数が違うので、真面目に音量調整しようとするとかなり苦労しそうです。上の動画では音声編集ツールを使ってある程度音量差を抑えていますが、それでも特定の音がかなりうるさく感じるでしょう。

MIDIファイルの解析には、MidiParserを使わせていただきました。このシンプルかつ強力なライブラリのおかげで、MIDIファイルの解析で特に困ったことはありませんでした。

自分の中で新たなチャレンジとして取り組んだのは、SwiftUIによるインタフェースの作成でした。VueやReactを使ったことがある人は割ととっつきやすいと思います。JavaScriptより型が厳密である分、SwiftUIの方が安心感があります。まだ発展途上の段階で、APIの追加・変更が多いので、もう少し落ち着くまで待つのも手だと思います。

　JoyKeyMapper v1.0.1 をリリースした / magicien　

JoyKeyMapperをアップデートしました。

修正内容は、
・一部のアプリで補助キーが効かない問題を修正
・App Storeの日本語対応
です。

キーの押下イベントを送信する時に、どの補助キーが押されているかのフラグを一緒に引数として渡しているのですが、Blender等の一部アプリでは、そのフラグを見ていないようで、補助キーの押下イベントを別途先に送っておく必要があるようです。例えば、Command+Zで取り消しするキー割り当てをしていた場合、

修正前：Zキー押下イベント＋Commandキーフラグ
修正後：Commandキー押下イベント、Zキー押下イベント＋Commandキーフラグ

のようになります。ボタンを離した時の処理も同様。
実際に使ってもらうと、色々と改善点が見つかりますね。今後も少しずつ改善していきたいです。

　Mac の Unreal Engine 4.25.1 でMMDモデル・モーションを一発で読み込む / magicien　

MMDモデル・モーションを読み込むUE4用プラグイン「IM4U」をMacに対応させた。
プラグインのダウンロードはここから。詳細は続きに。

（モデル：ロボ子さん（© 2019 cover corp.）、モーション：あざとかわいいターン）

オリジナルのIM4Uは既に開発停止してしまっているが、UE4.24向けにアップデートした方がいたので（tekifuta/IM4U）、これをMac UE4.25.1でビルドできるように修正した。（Mac UE 4.24 以前では動かないと思う）

インストール方法

今のところバイナリは配布していないので、プロジェクト毎にインストールする必要がある。

1. UE4.25.1のプロジェクトを作成する。
2. 作成したプロジェクトのパスに Plugins ディレクトリを作成する。（自分の環境だと、/Users/ユーザ名/Documents/Unreal Projects/プロジェクト名/Plugins）
3. Plugins ディレクトリの下に IM4U のGithubリポジトリを丸ごとダウンロードする。
（"git clone https://github.com/magicien/IM4U.git" コマンドか、Githubのページの "Clone or download" > "Download ZIP" でダウンロードしたZIPを展開する）
4. UEのプロジェクトを開き直すと、IM4Uをビルドするか聞かれるので、ビルドする。
5. あとは他のモデル・モーションファイルと同様にpmd/pmx/vmdファイルが読み込める。


以下はまだ対応できていないもの。後で対応するかもしれない。
・ルートボーンが無い（複数ある）PMDモデル対応
・モーション読み込み時にIKを適用する（UEにもIKの機能があるが、モーション自体にIK計算後のボーン位置を焼き込んだ方が良いだろう）
・物理演算対応（剛体だけだっけ？）
・英語対応（UI、コード中のコメント）
・リファクタリング

英語対応だけしておけば、残りは誰かが勝手にやってくれるかもしれない。

　Epic Online Services のAccount IDからProduct User IDを取得する / magicien　

「Epic Online Services のSDKでフレンドのプレゼンスを取得・監視する」の続き。

EOSでP2P通信するために、自分と相手のProduct User IDを指定する必要がある。ログイン・フレンド検索で使うIDは、Epic Account IDなので、Epic Account IDに紐づくProduct User IDを別途取得しないといけない。

よくよく調べると、このアカウント周りの処理は、やれることが多い分、処理内容もかなり複雑で、まだ理解しきれていない部分が多い。ライブラリ側でもう少し複雑さを隠蔽してくれてもいいのに。

今回は、一番簡単であろう、外部アカウントIDとして Epic Games を使った場合の流れについて。


まず、Epic Account ID と、Product User ID の関係を図にすると、次のようになる、はず。

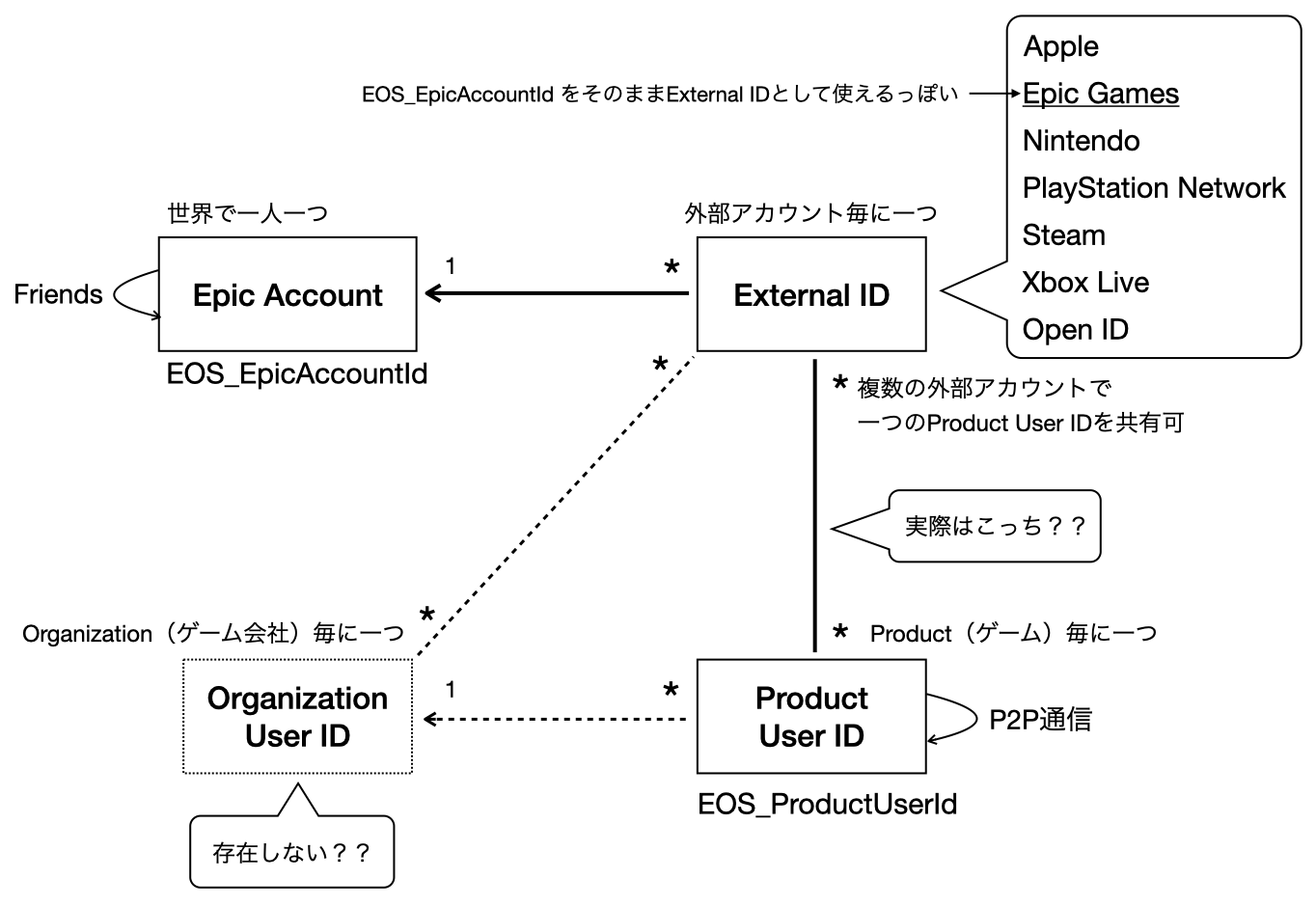
フレンドはEpic Account IDで管理されているが、P2P通信はゲームに紐づいたProduct User IDを指定する。そのため、フレンドとP2P通信をするには、Epic Account ID から Product User ID を取得しなければならない。

Epic Account ID

EpicのアカウントのIDは、Epic Gamesでユーザ登録すれば発行される。Epic Account IDは、ユーザに紐づくので、基本的に一人一つだけ割り当てられることになる。

Epic Account IDとExternal IDの関係

実は、Epic Gamesでユーザ登録しなくても、他のアカウント管理システムに紐づいて Epic Account ID の発行ができる。Apple、Nintendo、PSN、...で認証されたユーザのIDに紐付けて、Epic Account IDが発行される。外部アカウントのユーザID一つに紐づけられるEpic Account IDは一つだけ。逆に、一つの Epic Account ID を、複数の外部アカウントに紐付ける事はできる。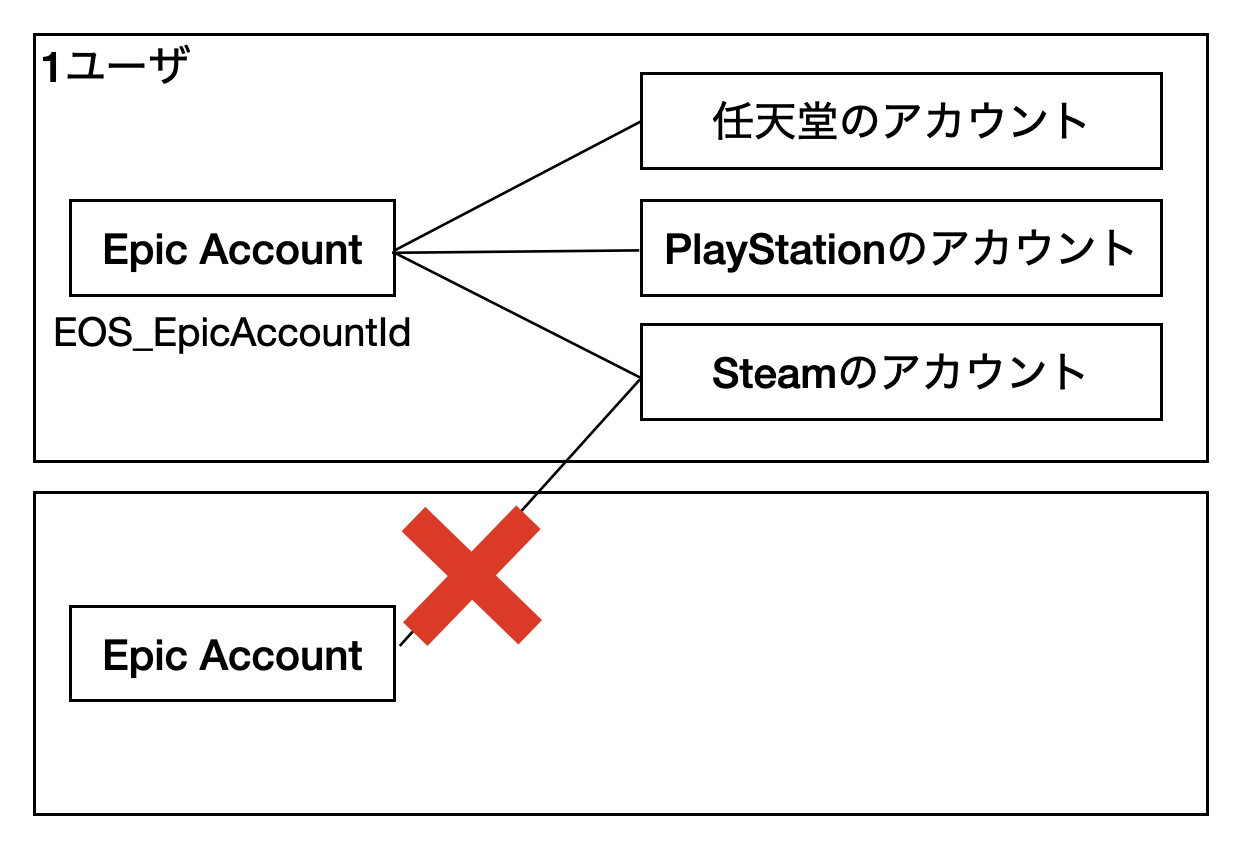

Organization User ID？

ドキュメントによると、Organization User IDなるものがあるらしい。が、SDK上にはそれらしいものが見当たらない。謎。
実際は、External IDからProduct User IDに紐づいているように思える。

External IDとProduct User IDの関係

Product User IDは、ゲーム毎に発行されるユーザID。External ID一つにつき、Product User IDが一つ紐づく。複数のExternal IDで一つのProduct User IDが共有できる。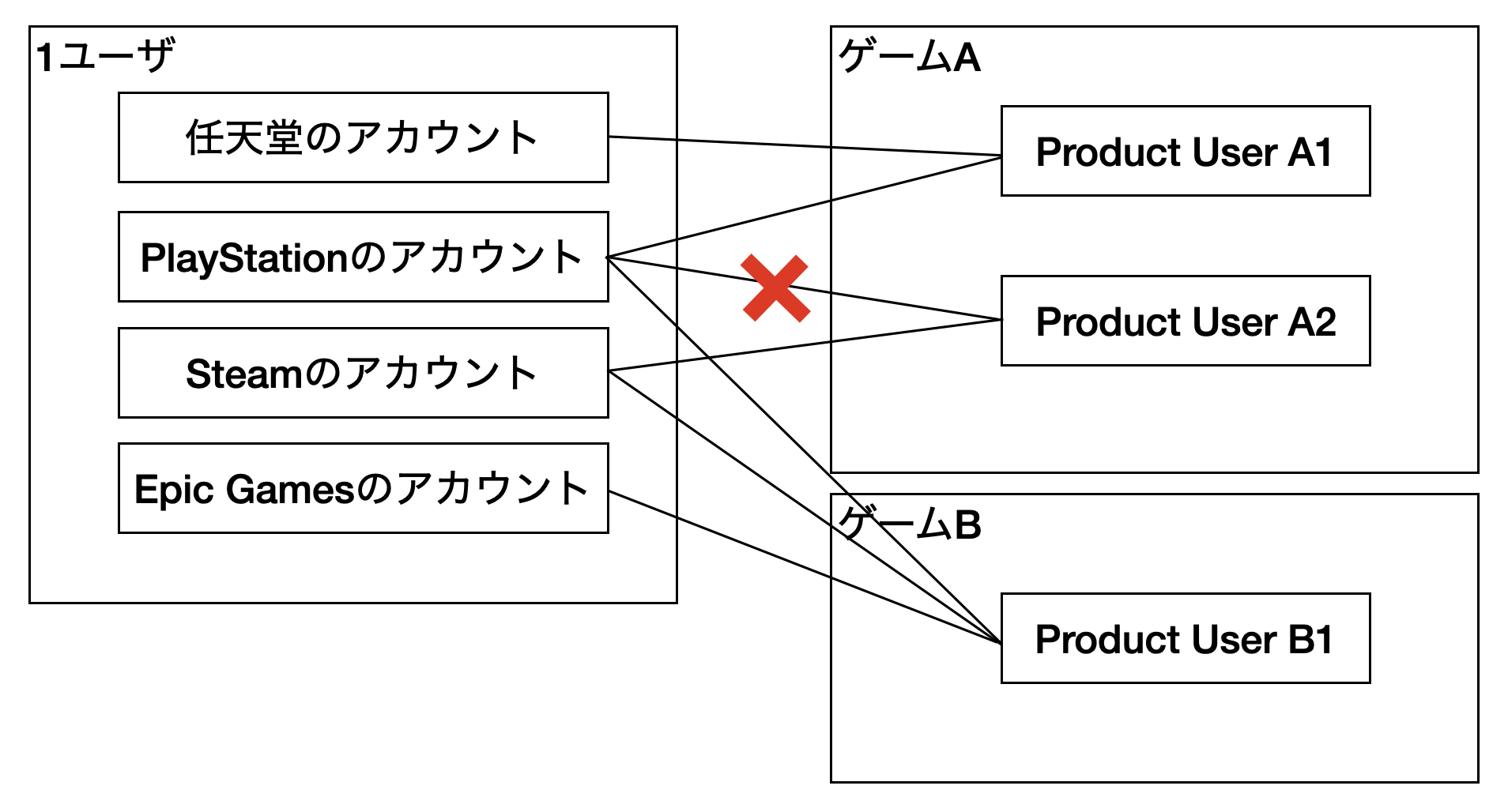

※PSのIDとゲームA用のProduct User ID（Product User A1）が既に紐づいている場合は、同じゲーム内で別のProduct User ID（Product User A2）に紐づけることはできない。

ユーザ、フレンドのEpic Account IDからProduct User IDを取得する

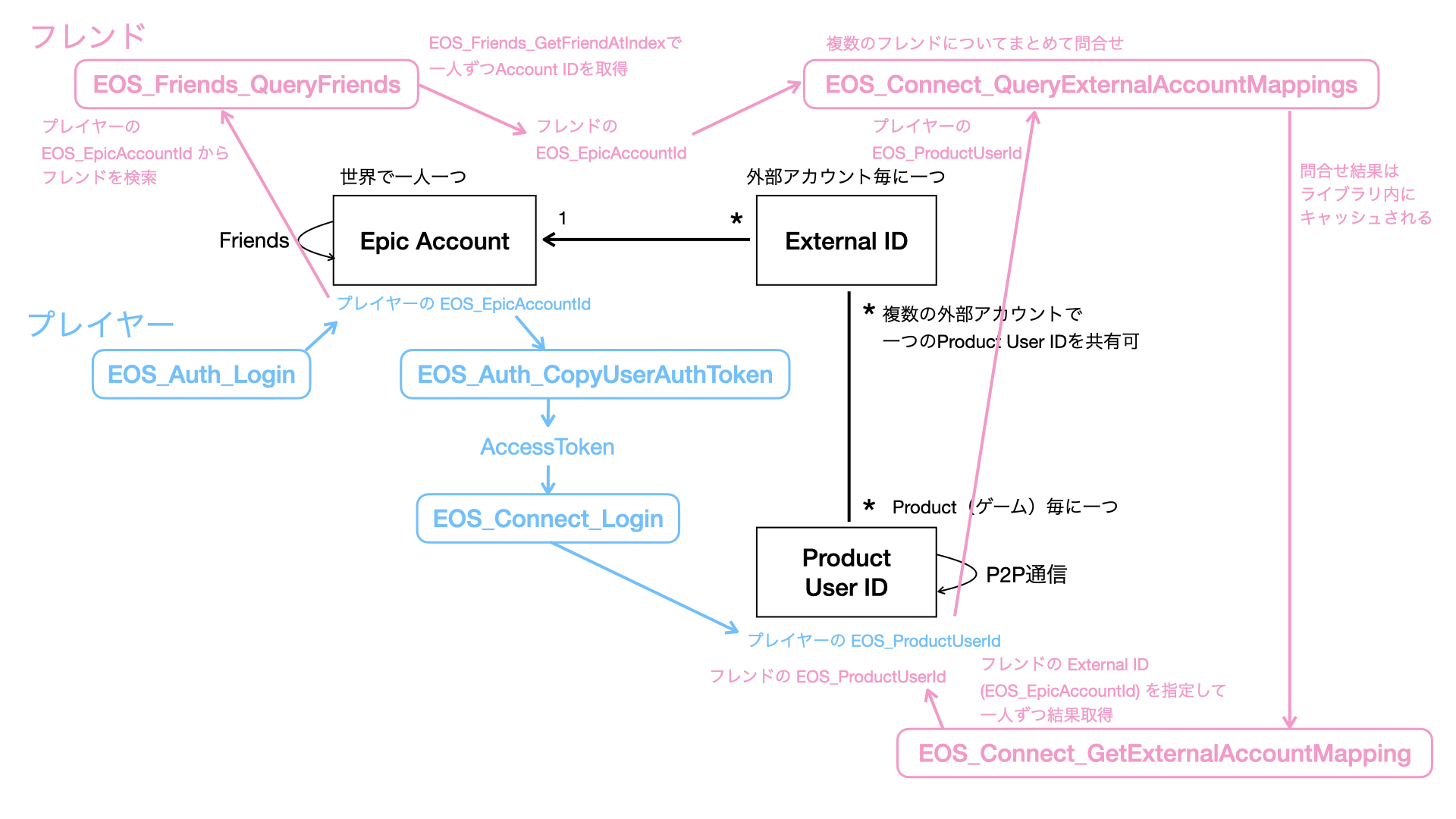
プレイヤー（Local User）のEpic Account IDは、ログイン時に取得できる。
さらに、Account IDからアクセストークンを取得、EOS_Connect_Loginにアクセストークンと外部アカウント（今回はEpic Games）を指定することで、プレイヤーのProduct User IDが取得できる。

フレンドのEpic Account IDは、EOS_Friends_QueryFriends のフレンド検索結果から得られる。この Epic Account ID を、外部アカウントのIDとして使う。EOS_Connect_QueryExternalAccountMappings に フレンドの Epic Account ID と、ユーザの Product User ID を渡して、フレンドの Product ID を取得する。
EOS_Connect_QueryExternalAccountMappings には、複数のフレンドの外部アカウントIDを渡せるので、一回のクエリでProduct User IDをまとめて取得できる。


文章にしようとすると、かなり複雑になってしまう。本当は、プレイヤーのProduct User IDが無い場合に、EOS_Connect_CreateUser でIDを作らないといけなかったり、既存のProduct User IDに外部アカウントを関連づけるために EOS_Connect_LinkAccount を呼んだりする場合があって、より複雑になる。（公式ドキュメント参照）

今回はここまで。

　JoyKeyMapper がフランス語で紹介されていた / magicien　

先日公開した JoyKeyMapper がフランス語で紹介されていました。ありがとうございます！
JoyKeyMapper Mac – Manettes de Jeu en Souris et Clavier (gratuit)


Google先生に頼りながら読んだ感じだと、ちゃんと使ってレビューしてくれたみたいで嬉しいです。Switchの発売から3年以上経って、今さらツールを作っても微妙かな、と思っていたのですが、過去に作られたツールは最新のOSで動かなかったりするようで、後発には後発のメリットがあるようです。

　Epic Online Services のSDKでフレンドのプレゼンスを取得・監視する（Swift） / magicien　

「Epic Online Services のSDKでログインしたユーザの情報を取得する」の続き。
フレンドのプレゼンス（オンライン・オフラインの状態、「〜をプレイ中」みたいなテキスト）を取得・監視する。

大まかな流れ

1. フレンド一覧を取得するクエリを発行する。
2. 取得したフレンドID一覧を基にさらに情報取得する（今回はプレゼンスを取得するクエリを発行する）。また、プレゼンスの変更を監視する。
3. プレゼンス取得結果を確認する。
4. プレゼンスに変更があった場合にこの関数が呼ばれる。

プレゼンスの監視対象が自分だけなのか、フレンドも含まれるかが未確認。（確認後に記事を更新予定）

上記コードには処理を書いていないが、不要になった監視は、EOS_Presence_RemoveNotifyOnPresenceChanged で止める必要がある。

追記１（5/31）：現状、同じOrganizationに登録されているユーザしかフレンドとして認識されないようだ。アプリの審査が通れば、他のユーザもフレンドとして認識されるのかもしれない。
追記２（6/5）：ドキュメントにアプリの審査が通るまで同じOrganizationのユーザとしかやりとりできない旨が書いてあった。（"Initially, you will only be able to interact with other users within your organization. After your application has passed review, it can be distributed to any users within the Epic ecosystem.")
今回はここまで。

続き：Epic Online Services のAccount IDからProduct User IDを取得する

　Epic Online Services のSDKでログインしたユーザの情報を取得する（Swift） / magicien　

「Epic Online Services のSDKでログインするまでの流れ」の続き。
ログインしたユーザの情報を取得する。

大まかな流れ

1. ログインする（前回の内容）
2. ログインしたユーザのIDを取得する
3. ユーザの情報を取得するためのクエリを送る
4. クエリの結果を取得する

ログインの時に EOS_Platform_GetAuthInterface(platformHandle) で EOS_Auth_XXX の関数呼び出しに必要なハンドルを取得したように、ユーザ関連の EOS_UserInfo_XXX の関数呼び出しに必要なハンドルは EOS_Platform_GetUserInfoInterface(platformHandle) で取得する。
他の関数の場合も同じように機能（Interface）毎にハンドルを取得する必要があるようだ。取得したハンドルをキャッシュして使いまわして良いかどうかは不明。
（Interface一覧は公式のドキュメント参照：Interfaces | Epic Online Services）
EOS_Auth_GetLoggedInAccountsCount は、これまでにログインしたアカウントの数を返す関数のようだけれど、Macで使うケースはあまり無いかもしれない。PS4のようなコンシューマ機なら一つのマシンで二人同時ログインするような用途は考えられる。

情報取得の際に渡すオプションの "LocalUserId" は、ログイン中のユーザID（リクエスト送信者）、"TargetUserId" は、情報取得対象のユーザID。今回は、ログインしたユーザ自身の情報を取得したいので、TargetUserIdにも自分のIDを指定している。

追記：EOS_UserInfo_CopyUserInfo でコピーしたデータは、EOS_UserInfo_Release で明示的に解放する必要があるっぽい。

今回はここまで。

続き：Epic Online Services のSDKでフレンドのプレゼンスを取得・監視する