- 2024年10月
- 2021年5月
- 2020年8月
- 2020年6月
- 2020年5月
- 2019年1月
- 2018年8月
- 2018年6月
- 2018年5月
- 2018年3月
- 2018年1月
- 2017年12月
- 2017年11月
- 2017年10月
- 2017年9月
- 2017年8月
- 2017年7月
- 2017年6月
- 2016年11月
- 2013年9月
- 2013年8月
- 2013年6月
- 2013年5月
- 2013年4月
- 2013年3月
- 2013年2月
- 2013年1月
- 2012年12月
- 2012年11月
- 2012年10月
- 2012年9月
- 2012年6月
- 2012年5月
- 2012年4月
- 2012年2月
- 2011年7月
- 2011年5月
- 2011年4月
- 2011年2月
- 2010年12月
- 2010年11月
- 2010年10月
- 2010年9月
- 2010年8月
- 2010年7月
- 2010年6月
- 2010年5月
- 2010年4月
- 2010年3月
- 2010年2月
- 2010年1月
- 2009年12月
- 2008年2月
- 2008年1月
- 2007年12月
- 2007年5月
- 2007年4月
- 2007年3月
- 2007年2月
macOSをアップデートしたら辞書データが消えました / magicien
Missing dictionaries for Dictionary app in 10.13.4 beta (17E139j)バージョンは、10.13.4 Beta 1。辞書をよく使う人は次のバージョンが出るまでアップデートを待った方が良いかもしれない。
割と使っているから早く直してくれ〜。AppleのQAチームが息してないぞ。
追記:手動でデータをダウンロードして復旧できた。原因は辞書データのダウンロード先がhttpであること(httpsではないこと)な気がする。
/System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xml に辞書一覧が入っているようだったので、
$ plutil -p /System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xmlで中身を見て、手動でデータダウンロードしたら復旧できました...
辞書一覧データの中身は配列になっていて、__BaseURL と __RelativePath をつなげたURLに辞書データが置いてある模様。
例えば、ウィズダム英和辞典の場合は、
11 => {
"__BaseURL" => "http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/"
"__CanUseLocalCacheServer" => 1
"__InstallWithOS" => 1
"__RelativePath" => "com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zip"
"_CompatibilityVersion" => 5
"_CompressionAlgorithm" => "zip"
"_ContentVersion" => 5
"_DownloadSize" => 29800639
"_IsZipStreamable" => 1
"_MasteredVersion" => "2610"
"_Measurement" => <41bb8766 3a4e0a5f a296262d 5fd506a4 bae32e1e>
"_MeasurementAlgorithm" => "SHA-1"
"_UnarchivedSize" => 33202176
"Countries" => [
0 => "JP"
]
"DictionaryCopyright" => "ウィズダム英和辞典 / The Wisdom English-Japanese Dictionary <br/> Copyright © 2007, 2013 Sanseido Company Ltd., under licence
to Oxford University Press. All rights reserved. <br/><br/> ウィズダム和英辞典 / The Wisdom Japanese-English Dictionary <br/> Copyright © 2007, 2013 Sanseido
Company Ltd., under licence to Oxford University Press. All rights reserved."
"DictionaryIdentifier" => "com.apple.dictionary.ja-en.WISDOM"
"DictionaryPackageDisplayName" => "ウィズダム英和辞典 / ウィズダム和英辞典"
"DictionaryPackageName" => "Sanseido The WISDOM English-Japanese Japanese-English Dictionary.dictionary"
"DictionaryType" => "Bilingual"
"FormatVersion" => 2
"IndexLanguages" => [
0 => "ja"
1 => "en"
]
"Language" => "ja"
}
となっているので、辞書データは
http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zipにある、という感じです。
ダウンロードしたzipファイルの中にある、〜.dictionary というファイルを ~/Library/Dictionaries/ に放り込んで、辞書アプリの環境設定から使う辞書に指定してあげればOK。
抽出したURL一覧を置いておきます。
辞書一覧
macOS用
Apple DictionaryPolitikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer's Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Dicionário de Português licenciado para Oxford University Press
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük
iOS用
Apple DictionaryPolitikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer’s Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Oxford Portuguese Dictionary - Português-Inglês • Inglês-Português
Dicionário de Português licenciado para Oxford University Press
Oxford Russian Dictionary - Русско-Английский • Англо-Русский
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük
タグ:
この記事のURL: https://darkhorse2.0spec.jp/257/
2018/01/28(Sun) 15:05:08
あけましておめでとうございます! / magicien
本年もよろしくお願いいたします。投稿遅くなっちゃったけどぎりぎりセーフ?
今年の10の目標はこんな感じで行きたいと思います。
- 初のiPhoneアプリをリリースする
- iPhoneのゲームアプリをリリースする
- AI関連の何かを作る
-
各種ライブラリの更新
- GLTFSceneKit:非同期読み込み対応、Exporter実装
- MMDSceneKit:物理演算対応、Exporter実装
- JSceneKit:Fox2サンプル対応、Exporter実装
- 新しいプログラミング言語を2つ習得
- 運動系イベントに参加する
- 何かしら絵を描く
- 何かしら曲を作る
- 何かしら得意料理を作る
- 今年始まった新しい何かに挑戦する
前半を書いたところで、ジャンル偏りすぎじゃね?っていうかライブラリに至っては目標というより予定じゃね?と思ったので後半はもうちょっと脳細胞が元気になりそうなものにしました。内容曖昧すぎじゃね?
今はiPhoneアプリを絶賛デバッグ中です。まだまだバグが多いのと、性能的に問題ありそうなんでリリースまでもうちょっとかかりそう。本当は昨年中に審査申請したかったんだけどなー。でも一度リリースまで経験すれば、次からはもっと早く作れる気がする。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/256/
2018/01/03(Wed) 18:19:56
クォータニオンの除算 / magicien
3Dのプログラムを書く人にとっては常識なのかもしれないけど、クォータニオンの除算ってどうやればいいんだっけと半日悩んだ結果を書いておく。結論から言うと、除算は不要。回転角度の符号を反転したクォータニオンを乗算すればいいだけでした。考えてみれば当然なんだけど、思いつかなかったんだよ!
そもそもクォータニオンは何かと言うと、回転を表す4次元ベクトル。クォータニオンの便利なところは、クォータニオン同士を乗算することで、回転を合成できること。
右肩、右肘、右手首の回転がそれぞれわかっている時に、最終的に右手がどっちの方向を向くかは、右肩・右肘・右手首のクォータニオンを全部乗算すれば分かる。
数式で表すなら、右肩のクォータニオンをq1、右肘のクォータニオンをq2、右手首のクォータニオンをq3、最終的に右手が向く方向をqとすると、
\( q_1 \times q_2 \times q_3 = q \)
こんな感じになるわけです(q1、q2、q3はローカルの回転、qはワールド座標系(正確には右肩の親ノード)から見た回転であることに要注意)。
じゃあ、右肩・右肘の回転が決まっていて、最終的に右手をどちらに向かせたいか決まっているときに、右手首をどう回転すれば良いのか計算で求めるには、どうすれば良いのかな?と思ったわけです。(q1、q2、qが既知の時にq3を求める)
回転方向を逆にしたクォータニオンを使えば良いのだけれど、これを共役(きょうやく)クォータニオンと呼ぶらしい。w成分の符号を反転させるか、xyzを反転させるか、どっちでも良いと思うのだけど、xyzを反転するのが正式なのかなぁ。記号の書き方も人によってまちまちだけど、ここでは、クォータニオンqの共役クォータニオンをq*と書くことにする。
\( q = (x, y, z, w) \Leftrightarrow q^* = (-x, -y, -z, w) \)
で、qとq*をぶつけてやれば、回転が無かったことになるので、
\( q_2^* \times q_1^* \times q_1 \times q_2 \times q_3 = q_2^* \times q_1^* \times q \\ \Leftrightarrow q_3 = q_2^* \times q_1^* \times q \)
という感じで q3 が求められる。クォータニオンの積の計算は結構複雑なので、下手に方程式を解き始める前に気づいて良かった...
おまけ:SceneKitのクォータニオンの積はこんな感じ。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/255/
2017/12/31(Sun) 05:54:25
iPhone Xを買った / magicien
 昨日、ふらっとApple Storeに行ったら、iPhone Xあるよって言うものだから買ってしまいました。
昨日、ふらっとApple Storeに行ったら、iPhone Xあるよって言うものだから買ってしまいました。iPhone Xを持ってる人たちが楽しそうにAnimojiやってるのを指をくわえて見ていたんですが、このままではくわえた指が溶けてしまう、と思って買っちゃうことにしました。
早速MMDのモデルを使ってFaceTrackingしてみたんですが、思った以上にすごいですわ。側から見た絵面が。おっさんがカメラに向かってウィンクしている様を想像してみてください。
ちょっと遊ぶつもりで作り始めたんですが、思いの外楽しいので、iOS向けアプリとして公開するのを目指すのもありかな、と考えているところです。ソースを公開したところで使える人はほんの一握りになっちゃうでしょうし。ただ、個人でアプリ公開したことないんで、勝手がわからないんですけどね...
公開するとなると、MMD関連ファイルのサポートを含めるかどうかも悩みどころ。大半のモデルがMMD以外での使用を想定されていないようなのと、権利的にグレーなものが多すぎるので、いらぬトラブルを呼び込むはめになりそう。
今は dae、obj、usd、glTF と他の選択肢も増えたので、MMDは外部ソフトに任せて自己責任で、というのが堅実なやり方かなぁ。逆にfbxはサポートしたいけど、簡単な方法はあるだろうか。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/254/
2017/12/22(Fri) 05:52:52
SceneKitのクォータニオンをMMDのオイラー角に変換する / magicien
JSceneKitを実装するときに、オイラー角とクォータニオンを相互変換する式を計算したのだけれど、今回はSceneKitのクォータニオンをMMDのオイラー角に変換する必要があった。が、前回使った計算式はどこかに行ってしまったので、再計算しなければならなかった。今回は途中式を記録に残しておく。
前提
- orientation(クォータニオン)からeulerAngles(オイラー角)を直接計算するのではなく、orientation→rotation、rotation→eulerAnglesの二段階の変換をする。
- orientationとrotationの変換は簡単なので省略。計算式は以前書いたSceneKitの系を参照のこと。
- 今回は回転だけ気にするので、3x3行列で計算する。
計算に使う行列
SCNNode.rotation (Rx, Ry, Rz, Rw) に対応するtransform:※rotationのxyz軸は大きさ1に正規化される。
\( rotation = (R_x, R_y, R_z, R_w) \\ \Rightarrow \left( \begin{array}{ccc} R_x^2 (1-\cos R_w) + \cos R_w & R_xR_y(1-\cos R_w) + R_z\sin R_w & R_xR_z(1-\cos R_w) - R_y\sin R_w \\ R_yR_x(1-\cos R_w) - R_z\sin R_w & R_y^2(1-\cos R_w) + \cos R_w & R_yR_z(1-\cos R_w) + R_x\sin R_w \\ R_zR_x(1-\cos R_w) + R_y\sin R_w & R_zR_y(1-\cos R_w) - R_x\sin R_w & R_z^2 (1-\cos R_w) + \cos R_w \end{array} \right) \tag{1} \)
SCNNode.eulerAngles (Ex, 0, 0) に対応するtransform:
\( eulerAngles = (E_x, 0, 0) \Rightarrow \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E_x & \sin E_x \\ 0 & -\sin E_x & \cos E_x \end{array} \right) \tag{2} \)
SCNNode.eulerAngles (0, Ey, 0) に対応するtransform:
\( eulerAngles = (0, E_y, 0) \Rightarrow \left( \begin{array}{ccc} \cos E_y & 0 & -\sin E_y \\ 0 & 1 & 0 \\ \sin E_y & 0 & \cos E_y \end{array} \right) \tag{3} \)
SCNNode.eulerAngles (0, 0, Ez) に対応するtransform:
\( eulerAngles = (0, 0, E_z) \Rightarrow \left( \begin{array}{ccc} \cos E_z & \sin E_z & 0 \\ -\sin E_z & \cos E_z & 0 \\ 0 & 0 & 1 \end{array} \right) \tag{4} \)
eulerAnglesのxyz回転を全て指定した場合は、SceneKitの場合、Z軸・Y軸・X軸の順番で回転する。回転行列は左側から掛けるので、次のようになる(この式は使わないけど、補足として)。
\( eulerAngles = (E_x, E_y, E_z) \Rightarrow \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E_x & \sin E_x \\ 0 & -\sin E_x & \cos E_x \end{array} \right) \left( \begin{array}{ccc} \cos E_y & 0 & -\sin E_y \\ 0 & 1 & 0 \\ \sin E_y & 0 & \cos E_y \end{array} \right) \left( \begin{array}{ccc} \cos E_z & \sin E_z & 0 \\ -\sin E_z & \cos E_z & 0 \\ 0 & 0 & 1 \end{array} \right) \tag{5} \)
MMDのカメラモーション(vmd)のオイラー角をSceneKitで再現する場合は、Z軸・-X軸・-Y軸の順で回転する必要がある。よって、回転行列は次のようになる。
\( MMDeulerAngles = (E'_x, E'_y, E'_z) \\ \Rightarrow eulerAngles(0, -E'_y, 0) \times eulerAngles(-E'_x, 0, 0) \times eulerAngles(0, 0, E'_z) \\ = \left( \begin{array}{ccc} \cos E'_y & 0 & \sin E'_y \\ 0 & 1 & 0 \\ -\sin E'_y & 0 & \cos E'_y \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E'_x & -\sin E'_x \\ 0 & \sin E'_x & \cos E'_x \end{array} \right) \left( \begin{array}{ccc} \cos E'_z & \sin E'_z & 0 \\ -\sin E'_z & \cos E'_z & 0 \\ 0 & 0 & 1 \end{array} \right) \\ = \left( \begin{array}{ccc} \cos E'_y \cos E'_z - \sin E'_x \sin E'_y \sin E'_z & \cos E'_y \sin E'_z + \sin E'_x \sin E'_y \cos E'_z & \cos E'_x \sin E'_y \\ - \cos E'_x \sin E'_z & \cos E'_x \cos E'_z & - \sin E'_x \\ - \sin E'_y \cos E'_z - \sin E'_x \cos E'_y \sin E'_z & - \sin E'_y \sin E'_z + \sin E'_x \cos E'_y \cos E'_z & \cos E'_x \cos E'_y \end{array} \right) \tag{6} \)
SceneKitのrotationをMMDのeulerAnglesに変換
rotation(Rx, Ry, Rz, Rw) から MMDeulerAngles(E'x, E'y, E'z) を求める。rotationとMMDeulerAnglesの回転行列を一致させてあげれば良いので、(1) = (6)より、
\( \left( \begin{array}{ccc} R_x^2 (1-\cos R_w) + \cos w & R_xR_y(1-\cos R_w) + R_z\sin R_w & R_xR_z(1-\cos R_w) - R_y\sin R_w \\ R_yR_x(1-\cos R_w) - R_z\sin w & R_y^2(1-\cos R_w) + \cos R_w & R_yR_z(1-\cos R_w) + R_x\sin R_w \\ R_zR_x(1-\cos R_w) + R_y\sin w & R_zR_y(1-\cos R_w) - R_x\sin R_w & R_z^2 (1-\cos R_w) + \cos R_w \end{array} \right) \\ = \left( \begin{array}{ccc} \cos E'_y \cos E'_z - \sin E'_x \sin E'_y \sin E'_z & \cos E'_y \sin E'_z + \sin E'_x \sin E'_y \cos E'_z & \cos E'_x \sin E'_y \\ - \cos E'_x \sin E'_z & \cos E'_x \cos E'_z & - \sin E'_x \\ - \sin E'_y \cos E'_z - \sin E'_x \cos E'_y \sin E'_z & - \sin E'_y \sin E'_z + \sin E'_x \cos E'_y \cos E'_z & \cos E'_x \cos E'_y \end{array} \right) \tag{7} \) で、E'x、E'y、E'zをRx、Ry、Rz、Rwで表せれば良いという寸法。
まずは E'x から。(7)の両辺の 2行3列目を取ると、
\( R_yR_z(1-\cos R_w) + R_x\sin R_w = - \sin E'_x \tag{8} \)
よって、
\( E'_x = \arcsin{(- R_yR_z(1-\cos R_w) - R_x\sin R_w)} \tag{9} \)
次は E'y。(7)の 1行3列目 / 3行3列目 を計算すると、
\( \frac{ R_xR_z(1-\cos R_w) - R_y\sin R_w }{ R_z^2 (1-\cos R_w) + \cos R_w } = \frac{ \cos E'_x \sin E'_y }{ \cos E'_x \cos E'_y } \tag{10} \)
よって、
\( E'_y = \arctan \frac{ R_xR_z(1-\cos R_w) - R_y\sin R_w }{ R_z^2 (1-\cos R_w) + \cos R_w } \tag{11} \)
最後に E'z。(7)の 2行1列目 / 2行2列目 を計算すると、
\( \frac{ R_yR_x(1-\cos R_w) - R_z\sin R_w }{ R_y^2(1-\cos R_w) + \cos R_w } = \frac{ - \cos E'_x \sin E'_z }{ \cos E'_x \cos E'_z } \tag{12} \) よって、
\( E'_z = \arctan \left( - \frac{ R_yR_x(1-\cos R_w) - R_z\sin R_w }{ R_y^2(1-\cos R_w) + \cos R_w } \right) \tag{13} \)
これでMMDのオイラー角が全て求められた。ちなみに、E'x が直角だと、cosE'x が 0 になり、(10)、(12)の右辺分母が0になってしまう。ので、別の方法で計算しないといけない(計算方法を忘れたので続きはまた今度)。
E'xが直角だと何が起こるかというと、 Z軸・-X軸・-Y軸の順で回転させた結果、X軸回転後にY軸がもともとZ軸があった場所に来てしまう。Y軸を回してもZ軸を回しても結果は同じ、ということで答えが一意に定まらなくなる。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/253/
2017/12/20(Wed) 03:53:33
MMDSceneKitに物理演算を追加した / magicien
 寝癖すごいことになってますよ?
寝癖すごいことになってますよ?作ろうと思って放置していた物理演算を追加した。pmd、pmx単体で読み込む分には、剛体が正しく読み込まれるはず。モデルをcloneした時の処理が未修正のため、pmmは今のところ未対応。
問題は、SceneKitにbtGeneric6DofSpringConstraintに該当するSCNPhysicsBehaviorが存在しないこと。代わりにSCNPhysicsBallSocketJointを使ってみたけれど、回転角度に制限が入れられないので、髪がねじれ放題。そして、なぜか前髪もあらぬ方向へ。
SceneKitは明らかにBullet Physicsを使っているので、6DoFのAPIが裏に隠れているはず。ぜひ使わせて欲しいのだけれど、なぜか少しずつ小出しにされるので、まだ使えません!
場合によっては見た目が残念なことになるので、MikuMikuDanceQuickLookに物理演算を組み込むのは、まだやめておこう。
別途Constraintを追加してあげれば良いのかなぁ...そうするくらいなら、自分でBullet Physicsを組み込む方が早い気がする。
この記事のURL: https://darkhorse2.0spec.jp/252/
2017/12/18(Mon) 06:46:05
MikuMikuDanceQuickLookの動画を作った / magicien
ライブラリ公開と併せて作るはずだった動画をようやく投稿できた。Homebrewを使ったインストール方法を用意できると良かったんだけど、Githubで公開しているものをHomebrewにも登録する場合、リポジトリのスターが10以上あることが条件になっているので、登録できなかったのだ!
このプラグインに興味を持ってくれた人は、今すぐMikuMikuDanceQuickLookのリポジトリにスターを付けるんだっ!
タグ:
この記事のURL: https://darkhorse2.0spec.jp/251/
2017/12/10(Sun) 19:55:36
羽生竜王+永世七冠おめでとうございます! / magicien
永世七冠、タイトル99期なんてもはや棋士としてカンストしてしまっているけれども、これからのご活躍も応援しています!それにしても、歴史的瞬間を生中継で見られて本当に良かった。インターネットの発展に感謝せざるを得ない。
こうなると叡王戦が蛇足感あるけど、将棋界にとってはタイトルが増えるのは喜ばしいことなんでしょうね。いずれ羽生さんが永世叡王を獲るだろうしな!
そういえば、先日ニコニコ動画がボコボコにされていたけれど、相撲を生中継してみたり、将棋を盛り上げたりと、日本の文化の発展に寄与しているところが少なからずあると思うので、期待の裏返しだと思って、めげずに頑張って欲しいですね!
タグ:
この記事のURL: https://darkhorse2.0spec.jp/250/
2017/12/05(Tue) 18:10:39
MMD用QuickLookプラグインを作った / magicien
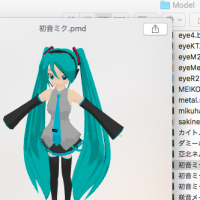 MMDはMikuMikuDanceの略です。念のため。
MMDはMikuMikuDanceの略です。念のため。MikuMikuDanceQuickLook - macOS QuickLook plugin for MikuMikuDance files
最初はMMDQuickLookっていう名前にしようと思っていたけれど、MultiMarkdown用プラグインと名前が被ったので変えました。
プラグインを使っていると、CPU使用率が高いまま張り付く現象が確認されています。OSを再起動するか、
kill -3 <QuickLookUIServiceのPID>で収まるんだけど、PID間違えると大変なことになるし、その後の動作に悪影響が出る可能性があるので、コマンドの意味が分かる人だけ自己責任でお願いします。
※以前、
kill -9と書いていたけれど、kill -3(SIGQUIT)でも終了できるみたいなので修正しました。こっちの方が幾分か安全かな。原因はQuickLookUIServiceのバグを疑っているけれど、その前に色々と検証せねば。
インストール方法
- GitHubのReleasesからzipファイル(MikuMikuDanceQuickLook_vX.X.X.zip)をダウンロードする
- zip内の MikuMikuDanceQuickLook.qlgenerator を /Library/QuickLook (全ユーザ用)か ~/Library/QuickLook(個別ユーザ用)にコピーする
- ターミナルで、qlmanage -r コマンドを実行(あるいは、OS再起動)して、QuickLookプラグインのリロードを行う。
対応フォーマット
- PMD
- PMX
- X
使い方
Finderでファイルを選ぶと、プレビュー欄に3Dモデルが表示されるよ!ファイル選択中にスペースキーを押すと、大きなプレビュー画面が表示されるよ!
※マウスでモデルを動かせるよ!
この記事のURL: https://darkhorse2.0spec.jp/249/
2017/11/27(Mon) 07:44:15
Xcodeのシーンエディタでシェーダのデバッグ中 / magicien
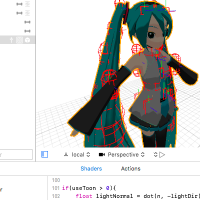 GLTFQuickLookについては、既に試していただいた方がいるようで、ありがたい限りです。
GLTFQuickLookについては、既に試していただいた方がいるようで、ありがたい限りです。が、本当に作りたいのは、MMD用のQuickLookなのです。
読み込んだモデルを一旦scnファイルに書き出す、という作戦に気づいた結果、シェーダのデバッグがしやすくなった。
シーンエディタを使えば、シェーダの編集結果がリアルタイムに反映されて、エラーや警告のある行も表示してくれる。
剛体の角度がうまく設定できていないな...というのも一目瞭然。
glTFと違って、MMDは対応する必要のあるファイルフォーマットがたくさんあって腕が鳴るぜぇ。
タグ:
この記事のURL: https://darkhorse2.0spec.jp/248/
2017/11/24(Fri) 20:07:17