タグに「雑記」を持つ
1〜10件目 / 79件
1 2 3 4 5 6 7 8 次へ

　しぐれういさんの個展に行った / magicien　

気づいたら3年半以上更新するのを忘れていた。仕事ばかりしていると、書けることが無くなってしまっていけない。先日、しぐれういさんの個展に行ったので、その日のことを書き残しておこうと思う。これは備忘とリハビリとサイトの動作確認のために、だらだらと書き連ねた自分のための文章なので、読む価値はあまり無い。

しぐれういさんは、言わずと知れたイラストレーター、そしてvtuberでもある。なぜか歌も歌っており、ある動画はYouTube上で1億再生を超えている。こうなると、もはや何者なのか分からなくなってくるが、本業はやはりイラストレーターであるということで、個展を開くという。

個展は六本木で開かれていた。週末、近くへ外出の予定があったため、ついでに寄ってみようと思い、昼に六本木の駅を降りた。9月の半ばになっても夏が我が物顔で居座っており、ヒルズに着く頃には汗が吹き出していた。遠目に長い行列が見えて嫌な予感がしていたのだが、近づいてみると案の定、個展の入場列ができている。このまま列に並ぶと、汗で全身びしょびしょの妖怪が個展会場に現れてしまう。入場までどれくらいかかるかもわからない。仕方ないので、個展は断念して本来の用事を先に済ませることにした。

平日に再挑戦しようとも考えたのだが、六本木はもしかして平日の方が人が多いかも知れないというのと、前職の関係者にばったり出くわしたらなんか嫌だなという思いがよぎり、夕方に再度個展会場に行ってみることにした。すると、入場列はなくなり代わりに整理券を配るスタッフが立っていた。薄暗くなった会場周辺では、個展の入り口を背景に写真撮影をしている人たちが多くいて、昼間とはまた違った雰囲気になっている。整理券を受け取り、数十分ほど森美術館の売店を冷やかした後、もう一度会場に行くと、すんなりと入場できた。

会場はシンメトリー、というか円形になっていて、半分がイラストレーター、もう半分がvtuberをテーマにした絵が並んでいる。個展というものにあまり行ったことがなかったため、それぞれの絵に値札が付いているのを見て、そういえば絵って買えるのかと、ふと思う。入り口に飾られている立体造形は 5,550,000 円となっていて、ほぼ原価だという。自分が個展を開いたらきっと破産してしまうだろう。

物販の列が出来ていることを除けば、会場内は思ったより混雑していなかったが、そこまで広々としたスペースがあるわけでもなく、自然、絵を至近距離から眺めることになる。考えてみると、パソコンで絵を観るときはもっと近いんだったと思いつつ、ディスプレイよりも大きなサイズのデジタル絵をどうやって描いたのだろうと思案する。会場内は暗めで、見上げると青や黄色のライトが絵に光を投げかけている。仕掛けのある絵が多く、光がオーロラのように反射したり、上層の絵が下層に影を作ったりと、リアルだからこその展示ばかりで、そういえば、しぐれういさんは美大出身であることを思い出した（高校生のはずだけど）。

この個展は、vtuberデビュー5周年企画の一部でもあり、同じく5周年企画で発売されたCDのジャケット絵も飾られていた。このCD自体にも数多くの著名なアーティストが関わっていて、CDを買ったときは、随分とどでかいことをしたな、とびっくりしたものだ。しかし、個展に並ぶ絵の一つとしてCDジャケット絵があるのを見ると、どでかく感じたCDは世界の一部で、外側にさらに大きな世界が広がっていることを思い知らされて呆然とした。

vtuberサイドには、様々なvtuberの絵が並んでいた。中でも目を惹いたのは、にじさんじのリゼ・ヘルエスタさんを描いたもの。背景が一部透明になっている絵に複数のライトが当たっていて、後ろの壁に映る髪の影に濃淡が生まれており、それがとても有機的で魅力的だった。個展のタイトルが「雨を手繰る」なのだが、リゼさんが雨女として知られており、その偶然の関係性にも感じるところがあった。

二重円のような構造の会場の中心部には、取り囲むようにディスプレイが並んでいて、Live2Dや3Dのしぐれういさんが時折、歩いたり座ったりする姿を見せる。上には大きな傘がかかっていて、雨が傘を叩く音が聞こえてくる。天井の青いライトは、この傘に空と雲を投影するためのものだったようだ。学校のチャイムと雨音をモチーフにしたようなピアノがBGMとして流れており、チルい。空調のおかげで温度的にもチルい。おかげで会場をぐるぐると何周もして、数々の絵と快適な空調に別れを告げられずにいた。

ゾーンはリアルのイラストレーターとバーチャルのvtuberとで分かれていたものの、何周もしているうちにその境目が曖昧に感じるようになった。影が光から生み出されるように、フィクションもリアルから生み出されたものであり、その境界は綺麗に切り分けられるものではなく、滲んで混ざる。どんなに否定しようと親子がその関係を取り消せないように、リアルとフィクションの関係は切り離せないのだ（JJ...）。CDのfictionというタイトルからそんなことを考えつつ、ゾンビのように会場を徘徊していた（疲れていたのかもしれない）。断腸の思いでようやく会場を出ると、外はすっかり暗くなっており、まだ蒸し暑い空気の向こうから微かに聞こえる虫の音は、秋の到来を予感させるものだった。

リアルで創作物に触れる機会は久しぶりで、密度の高い作品に触れると創作意欲がかきたてられる。とはいえ、絵を描くのは苦手なので、自分はコードを書いて欲を満たす他ない。最近はUnityに触れる機会が増えたので、Unityで何か作ってみたいとぼんやりと考えている。

せっかくなので、3周年記念の時に作ったファンアート的ウェブページも置いておこう。今見返してみても、我ながら頑張って作ったと思う。この時も同じように創作意欲に掻き立てられてものづくりに没頭していたのを覚えている。外からの刺激が自分へどれほど大きな影響を与えるかを今回改めて思い出すことができた。
https://magicien.github.io/CanvasInShower/

　あけましておめでとうございます / magicien　

生きています。


昨年の目標を見返してみたら、ほぼ達成できていませんでした。
vtuberが楽しすぎて、年始早々に軌道がずれていったようです。
2019年は昨年のような熱に浮かされた感じから徐々に落ち着いていくと思うので、目標達成率も上がるでしょう。
そんなわけで2019年の目標。

• サイト引越し
• vtuberデビューする
• glTF/VRM で何かしら貢献する
• SceneKit/ARKit で何かしら貢献する
• アプリ開発頑張る
• VR機器買って何か開発する（QuestかCosmosか...）
• 動画関連のソフトかサービスを作る
• 誰かと共同で何か作る
• 風邪をひかない（花粉症は仕方ない）
• 週次で何かやる

目標にする分野の範囲が狭すぎる。また今年も新しいものが出てくると思うので、その時に目標を考えよう。

　WWDC2018のKeynoteメモ / magicien　

Keynoteに一時間遅刻してしまった...ギル様を優先したとも言う。別言語で2窓は流石に無理だった。まだまだ修行が必要。

ただ、2時間のライブであれば、1時間の遅刻は遅刻にはならない。
YouTubeには便利な機能があって、ライブ中でも1時間遅れで再生出来るので、倍速で再生すれば、1時間後には最新の映像に追いつけるという寸法である。

さて、3D好きとしては、やはりARKit2に注目したい。
複数の端末で一つのAR空間を共有出来るのは非常に嬉しい。
背景を実写ではなく3Dモデルにすれば、VRも出来るので、顔認識用の人数分のiPhoneXとカメラモーション用のiPhone端末が用意できれば、同じVR空間で複数のVTuberがわちゃわちゃ動き回る様をライブ配信出来るようになりそう。ネット越しの同期もサポートしてくれるなら、物理的に集合する必要はない。出演者だけではなく、観客も同じ空間に入り込んで自由に動き回れる。どこまで出来そうかは後でAPIを確認しよう。
→確認した結果、ネット越しだとあんまり使えなさそう。表情の変化をリアルタイムに反映するのもだいぶ頑張らないといけないようだ。ライブラリにお任せ出来ると思ったのに、結局自分で実装しないといけないのか。

usdzというファイル形式は、usdの拡張でzip対応しているっぽい。ネット経由での利用を意識してのものだと思うので、glTFと競合していくことになるのかな。個人的にはVRMがglTFの公認拡張仕様になってglTFが流行って欲しい。

正直、他に気になるものがあまり無かった。あとはSessionのスケジュールを見て気になるものを選んで見ていけば良いかな、と考え中。ReplayKit 2、HLS、ARKit 2、Ray Tracing、Video Effects Using Depthあたり。MapKit JSも地味に気になる。あとはかなり望み薄だけど、SafariがWebGL2、GLES3に対応する気があるかどうか。
→OpenGL ESがdeprecatedって書いてある！WebGLをどうするつもりなんだ。

そういえば、MicrosoftがGitHubを買収するとかなんとか。アメリカのIT企業は他社のイベントに爆弾を放り込むノルマでもあるんですかね...

　macOSをアップデートしたら辞書データが消えました / magicien　

Missing dictionaries for Dictionary app in 10.13.4 beta (17E139j)
バージョンは、10.13.4 Beta 1。辞書をよく使う人は次のバージョンが出るまでアップデートを待った方が良いかもしれない。


割と使っているから早く直してくれ〜。AppleのQAチームが息してないぞ。

追記：手動でデータをダウンロードして復旧できた。原因は辞書データのダウンロード先がhttpであること（httpsではないこと）な気がする。

/System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xml に辞書一覧が入っているようだったので、

$ plutil -p /System/Library/Assets/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/com_apple_MobileAsset_DictionaryServices_dictionaryOSX.xml

で中身を見て、手動でデータダウンロードしたら復旧できました...
辞書一覧データの中身は配列になっていて、__BaseURL と __RelativePath をつなげたURLに辞書データが置いてある模様。
例えば、ウィズダム英和辞典の場合は、

11 => {
      "__BaseURL" => "http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/"
      "__CanUseLocalCacheServer" => 1
      "__InstallWithOS" => 1
      "__RelativePath" => "com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zip"
      "_CompatibilityVersion" => 5
      "_CompressionAlgorithm" => "zip"
      "_ContentVersion" => 5
      "_DownloadSize" => 29800639
      "_IsZipStreamable" => 1
      "_MasteredVersion" => "2610"
      "_Measurement" => <41bb8766 3a4e0a5f a296262d 5fd506a4 bae32e1e>
      "_MeasurementAlgorithm" => "SHA-1"
      "_UnarchivedSize" => 33202176
      "Countries" => [
        0 => "JP"
      ]
      "DictionaryCopyright" => "ウィズダム英和辞典 / The Wisdom English-Japanese Dictionary <br/> Copyright © 2007, 2013 Sanseido Company Ltd., under licence 
to Oxford University Press.  All rights reserved. <br/><br/> ウィズダム和英辞典 / The Wisdom Japanese-English Dictionary <br/> Copyright © 2007, 2013 Sanseido
 Company Ltd., under licence to Oxford University Press.  All rights reserved."
      "DictionaryIdentifier" => "com.apple.dictionary.ja-en.WISDOM"
      "DictionaryPackageDisplayName" => "ウィズダム英和辞典 / ウィズダム和英辞典"
      "DictionaryPackageName" => "Sanseido The WISDOM English-Japanese Japanese-English Dictionary.dictionary"
      "DictionaryType" => "Bilingual"
      "FormatVersion" => 2
      "IndexLanguages" => [
        0 => "ja"
        1 => "en"
      ]
      "Language" => "ja"
    }

となっているので、辞書データは

http://appldnld.apple.com/osxassets/058-55450-2016008023-8A4D782E-661F-11E6-B483-D75733D2D062/com_apple_MobileAsset_DictionaryServices_dictionaryOSX/1a184f41ee27bbb203ba596a25c8ea104c13d98f.zip

にある、という感じです。
ダウンロードしたzipファイルの中にある、〜.dictionary というファイルを ~/Library/Dictionaries/ に放り込んで、辞書アプリの環境設定から使う辞書に指定してあげればOK。
抽出したURL一覧を置いておきます。

辞書一覧

macOS用

Apple Dictionary
Politikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer's Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Dicionário de Português licenciado para Oxford University Press
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük

iOS用

Apple Dictionary
Politikens Nudansk Ordbog
Prisma Handwoordenboek Engels
Prisma woordenboek Nederlands
Oxford-Hachette French Dictionary
Multidictionnaire de la langue française
Oxford German Dictionary
Duden-Wissensnetz deutsche Sprache
राजपाल हिन्दी शब्दकोश
Oxford Paravia Il Dizionario inglese - italiano/italiano - inglese
Dizionario italiano da un affiliato di Oxford University Press
ウィズダム英和辞典 / ウィズダム和英辞典
スーパー大辞林
뉴에이스 영한사전 / 뉴에이스 한영사전
뉴에이스 국어사전
Norsk Ordbok
New Oxford American Dictionary
Oxford American Writer’s Thesaurus
Oxford Dictionary of English
Oxford Thesaurus of English
Oxford Portuguese Dictionary - Português-Inglês • Inglês-Português
Dicionário de Português licenciado para Oxford University Press
Oxford Russian Dictionary - Русско-Английский • Англо-Русский
Толковый словарь русского языка
牛津英汉汉英词典
现代汉语规范词典
Gran Diccionario Oxford - Español-Inglés • Inglés-Español
Diccionario General de la Lengua Española Vox
NE Ordbok
พจนานุกรมไทย ฉบับทันสมัยและสมบูรณ์
五南國語活用辭典
TTY Dictionary
Arkadaş Türkçe Sözlük

　あけましておめでとうございます！ / magicien　

本年もよろしくお願いいたします。


投稿遅くなっちゃったけどぎりぎりセーフ？

今年の10の目標はこんな感じで行きたいと思います。

• 初のiPhoneアプリをリリースする
• iPhoneのゲームアプリをリリースする
• AI関連の何かを作る
• 各種ライブラリの更新
  • GLTFSceneKit：非同期読み込み対応、Exporter実装
  • MMDSceneKit：物理演算対応、Exporter実装
  • JSceneKit：Fox2サンプル対応、Exporter実装
• 新しいプログラミング言語を２つ習得
• 運動系イベントに参加する
• 何かしら絵を描く
• 何かしら曲を作る
• 何かしら得意料理を作る
• 今年始まった新しい何かに挑戦する

前半を書いたところで、ジャンル偏りすぎじゃね？っていうかライブラリに至っては目標というより予定じゃね？と思ったので後半はもうちょっと脳細胞が元気になりそうなものにしました。内容曖昧すぎじゃね？

今はiPhoneアプリを絶賛デバッグ中です。まだまだバグが多いのと、性能的に問題ありそうなんでリリースまでもうちょっとかかりそう。本当は昨年中に審査申請したかったんだけどなー。でも一度リリースまで経験すれば、次からはもっと早く作れる気がする。

　クォータニオンの除算 / magicien　

3Dのプログラムを書く人にとっては常識なのかもしれないけど、クォータニオンの除算ってどうやればいいんだっけと半日悩んだ結果を書いておく。

結論から言うと、除算は不要。回転角度の符号を反転したクォータニオンを乗算すればいいだけでした。考えてみれば当然なんだけど、思いつかなかったんだよ！

そもそもクォータニオンは何かと言うと、回転を表す4次元ベクトル。クォータニオンの便利なところは、クォータニオン同士を乗算することで、回転を合成できること。
右肩、右肘、右手首の回転がそれぞれわかっている時に、最終的に右手がどっちの方向を向くかは、右肩・右肘・右手首のクォータニオンを全部乗算すれば分かる。
数式で表すなら、右肩のクォータニオンをq1、右肘のクォータニオンをq2、右手首のクォータニオンをq3、最終的に右手が向く方向をqとすると、

\( q_1 \times q_2 \times q_3 = q \)

こんな感じになるわけです（q1、q2、q3はローカルの回転、qはワールド座標系（正確には右肩の親ノード）から見た回転であることに要注意）。
じゃあ、右肩・右肘の回転が決まっていて、最終的に右手をどちらに向かせたいか決まっているときに、右手首をどう回転すれば良いのか計算で求めるには、どうすれば良いのかな？と思ったわけです。（q1、q2、qが既知の時にq3を求める）

回転方向を逆にしたクォータニオンを使えば良いのだけれど、これを共役（きょうやく）クォータニオンと呼ぶらしい。w成分の符号を反転させるか、xyzを反転させるか、どっちでも良いと思うのだけど、xyzを反転するのが正式なのかなぁ。記号の書き方も人によってまちまちだけど、ここでは、クォータニオンqの共役クォータニオンをq*と書くことにする。

\( q = (x, y, z, w) \Leftrightarrow q^* = (-x, -y, -z, w) \)

で、qとq*をぶつけてやれば、回転が無かったことになるので、

\( q_2^* \times q_1^* \times q_1 \times q_2 \times q_3 = q_2^* \times q_1^* \times q \\ \Leftrightarrow q_3 = q_2^* \times q_1^* \times q \)

という感じで q3 が求められる。クォータニオンの積の計算は結構複雑なので、下手に方程式を解き始める前に気づいて良かった...

おまけ：SceneKitのクォータニオンの積はこんな感じ。

　SceneKitのクォータニオンをMMDのオイラー角に変換する / magicien　

JSceneKitを実装するときに、オイラー角とクォータニオンを相互変換する式を計算したのだけれど、今回はSceneKitのクォータニオンをMMDのオイラー角に変換する必要があった。
が、前回使った計算式はどこかに行ってしまったので、再計算しなければならなかった。今回は途中式を記録に残しておく。

前提

• orientation（クォータニオン）からeulerAngles（オイラー角）を直接計算するのではなく、orientation→rotation、rotation→eulerAnglesの二段階の変換をする。
• orientationとrotationの変換は簡単なので省略。計算式は以前書いたSceneKitの系を参照のこと。
• 今回は回転だけ気にするので、3x3行列で計算する。

計算に使う行列

SCNNode.rotation (Rx, Ry, Rz, Rw) に対応するtransform：
※rotationのxyz軸は大きさ1に正規化される。
\( rotation = (R_x, R_y, R_z, R_w) \\ \Rightarrow \left( \begin{array}{ccc} R_x^2 (1-\cos R_w) + \cos R_w & R_xR_y(1-\cos R_w) + R_z\sin R_w & R_xR_z(1-\cos R_w) - R_y\sin R_w \\ R_yR_x(1-\cos R_w) - R_z\sin R_w & R_y^2(1-\cos R_w) + \cos R_w & R_yR_z(1-\cos R_w) + R_x\sin R_w \\ R_zR_x(1-\cos R_w) + R_y\sin R_w & R_zR_y(1-\cos R_w) - R_x\sin R_w & R_z^2 (1-\cos R_w) + \cos R_w \end{array} \right) \tag{1} \)

SCNNode.eulerAngles (Ex, 0, 0) に対応するtransform：
\( eulerAngles = (E_x, 0, 0) \Rightarrow \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E_x & \sin E_x \\ 0 & -\sin E_x & \cos E_x \end{array} \right) \tag{2} \)

SCNNode.eulerAngles (0, Ey, 0) に対応するtransform：
\( eulerAngles = (0, E_y, 0) \Rightarrow \left( \begin{array}{ccc} \cos E_y & 0 & -\sin E_y \\ 0 & 1 & 0 \\ \sin E_y & 0 & \cos E_y \end{array} \right) \tag{3} \)

SCNNode.eulerAngles (0, 0, Ez) に対応するtransform：
\( eulerAngles = (0, 0, E_z) \Rightarrow \left( \begin{array}{ccc} \cos E_z & \sin E_z & 0 \\ -\sin E_z & \cos E_z & 0 \\ 0 & 0 & 1 \end{array} \right) \tag{4} \)

eulerAnglesのxyz回転を全て指定した場合は、SceneKitの場合、Z軸・Y軸・X軸の順番で回転する。回転行列は左側から掛けるので、次のようになる（この式は使わないけど、補足として）。
\( eulerAngles = (E_x, E_y, E_z) \Rightarrow \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E_x & \sin E_x \\ 0 & -\sin E_x & \cos E_x \end{array} \right) \left( \begin{array}{ccc} \cos E_y & 0 & -\sin E_y \\ 0 & 1 & 0 \\ \sin E_y & 0 & \cos E_y \end{array} \right) \left( \begin{array}{ccc} \cos E_z & \sin E_z & 0 \\ -\sin E_z & \cos E_z & 0 \\ 0 & 0 & 1 \end{array} \right) \tag{5} \)

MMDのカメラモーション（vmd）のオイラー角をSceneKitで再現する場合は、Z軸・-X軸・-Y軸の順で回転する必要がある。よって、回転行列は次のようになる。
\( MMDeulerAngles = (E'_x, E'_y, E'_z) \\ \Rightarrow eulerAngles(0, -E'_y, 0) \times eulerAngles(-E'_x, 0, 0) \times eulerAngles(0, 0, E'_z) \\ = \left( \begin{array}{ccc} \cos E'_y & 0 & \sin E'_y \\ 0 & 1 & 0 \\ -\sin E'_y & 0 & \cos E'_y \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos E'_x & -\sin E'_x \\ 0 & \sin E'_x & \cos E'_x \end{array} \right) \left( \begin{array}{ccc} \cos E'_z & \sin E'_z & 0 \\ -\sin E'_z & \cos E'_z & 0 \\ 0 & 0 & 1 \end{array} \right) \\ = \left( \begin{array}{ccc} \cos E'_y \cos E'_z - \sin E'_x \sin E'_y \sin E'_z & \cos E'_y \sin E'_z + \sin E'_x \sin E'_y \cos E'_z & \cos E'_x \sin E'_y \\ - \cos E'_x \sin E'_z & \cos E'_x \cos E'_z & - \sin E'_x \\ - \sin E'_y \cos E'_z - \sin E'_x \cos E'_y \sin E'_z & - \sin E'_y \sin E'_z + \sin E'_x \cos E'_y \cos E'_z & \cos E'_x \cos E'_y \end{array} \right) \tag{6} \)

SceneKitのrotationをMMDのeulerAnglesに変換

rotation(Rx, Ry, Rz, Rw) から MMDeulerAngles(E'x, E'y, E'z) を求める。
rotationとMMDeulerAnglesの回転行列を一致させてあげれば良いので、(1) = (6)より、
\( \left( \begin{array}{ccc} R_x^2 (1-\cos R_w) + \cos w & R_xR_y(1-\cos R_w) + R_z\sin R_w & R_xR_z(1-\cos R_w) - R_y\sin R_w \\ R_yR_x(1-\cos R_w) - R_z\sin w & R_y^2(1-\cos R_w) + \cos R_w & R_yR_z(1-\cos R_w) + R_x\sin R_w \\ R_zR_x(1-\cos R_w) + R_y\sin w & R_zR_y(1-\cos R_w) - R_x\sin R_w & R_z^2 (1-\cos R_w) + \cos R_w \end{array} \right) \\ = \left( \begin{array}{ccc} \cos E'_y \cos E'_z - \sin E'_x \sin E'_y \sin E'_z & \cos E'_y \sin E'_z + \sin E'_x \sin E'_y \cos E'_z & \cos E'_x \sin E'_y \\ - \cos E'_x \sin E'_z & \cos E'_x \cos E'_z & - \sin E'_x \\ - \sin E'_y \cos E'_z - \sin E'_x \cos E'_y \sin E'_z & - \sin E'_y \sin E'_z + \sin E'_x \cos E'_y \cos E'_z & \cos E'_x \cos E'_y \end{array} \right) \tag{7} \) で、E'x、E'y、E'zをRx、Ry、Rz、Rwで表せれば良いという寸法。


まずは E'x から。(7)の両辺の 2行3列目を取ると、
\( R_yR_z(1-\cos R_w) + R_x\sin R_w = - \sin E'_x \tag{8} \)
よって、
\( E'_x = \arcsin{(- R_yR_z(1-\cos R_w) - R_x\sin R_w)} \tag{9} \)

次は E'y。(7)の 1行3列目 / 3行3列目 を計算すると、
\( \frac{ R_xR_z(1-\cos R_w) - R_y\sin R_w }{ R_z^2 (1-\cos R_w) + \cos R_w } = \frac{ \cos E'_x \sin E'_y }{ \cos E'_x \cos E'_y } \tag{10} \)
よって、
\( E'_y = \arctan \frac{ R_xR_z(1-\cos R_w) - R_y\sin R_w }{ R_z^2 (1-\cos R_w) + \cos R_w } \tag{11} \)

最後に E'z。(7)の 2行1列目 / 2行2列目 を計算すると、
\( \frac{ R_yR_x(1-\cos R_w) - R_z\sin R_w }{ R_y^2(1-\cos R_w) + \cos R_w } = \frac{ - \cos E'_x \sin E'_z }{ \cos E'_x \cos E'_z } \tag{12} \) よって、
\( E'_z = \arctan \left( - \frac{ R_yR_x(1-\cos R_w) - R_z\sin R_w }{ R_y^2(1-\cos R_w) + \cos R_w } \right) \tag{13} \)

これでMMDのオイラー角が全て求められた。ちなみに、E'x が直角だと、cosE'x が 0 になり、(10)、(12)の右辺分母が0になってしまう。ので、別の方法で計算しないといけない（計算方法を忘れたので続きはまた今度）。
E'xが直角だと何が起こるかというと、 Z軸・-X軸・-Y軸の順で回転させた結果、X軸回転後にY軸がもともとZ軸があった場所に来てしまう。Y軸を回してもZ軸を回しても結果は同じ、ということで答えが一意に定まらなくなる。

　MikuMikuDanceQuickLookの動画を作った / magicien　

ライブラリ公開と併せて作るはずだった動画をようやく投稿できた。



Homebrewを使ったインストール方法を用意できると良かったんだけど、Githubで公開しているものをHomebrewにも登録する場合、リポジトリのスターが10以上あることが条件になっているので、登録できなかったのだ！
このプラグインに興味を持ってくれた人は、今すぐMikuMikuDanceQuickLookのリポジトリにスターを付けるんだっ！

　羽生竜王＋永世七冠おめでとうございます！ / magicien　

永世七冠、タイトル99期なんてもはや棋士としてカンストしてしまっているけれども、これからのご活躍も応援しています！


それにしても、歴史的瞬間を生中継で見られて本当に良かった。インターネットの発展に感謝せざるを得ない。
こうなると叡王戦が蛇足感あるけど、将棋界にとってはタイトルが増えるのは喜ばしいことなんでしょうね。いずれ羽生さんが永世叡王を獲るだろうしな！

そういえば、先日ニコニコ動画がボコボコにされていたけれど、相撲を生中継してみたり、将棋を盛り上げたりと、日本の文化の発展に寄与しているところが少なからずあると思うので、期待の裏返しだと思って、めげずに頑張って欲しいですね！

　Xcodeのシーンエディタでシェーダのデバッグ中 / magicien　

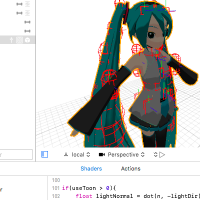GLTFQuickLookについては、既に試していただいた方がいるようで、ありがたい限りです。
が、本当に作りたいのは、MMD用のQuickLookなのです。

読み込んだモデルを一旦scnファイルに書き出す、という作戦に気づいた結果、シェーダのデバッグがしやすくなった。
シーンエディタを使えば、シェーダの編集結果がリアルタイムに反映されて、エラーや警告のある行も表示してくれる。
剛体の角度がうまく設定できていないな...というのも一目瞭然。

glTFと違って、MMDは対応する必要のあるファイルフォーマットがたくさんあって腕が鳴るぜぇ。